Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ
Α |
|---|
Ακέραια αλγεβρική παράστασηΜια αλγεβρική παράσταση λέγεται ακέραια, όταν μεταξύ των μεταβλητών της
Για παράδειγμα η παράσταση $$\sqrt 2 {x^2} - \frac{2}{3}x$$ είναι ακέραια ενώ η $$2\sqrt x + 5x$$ δεν είναι. | |
Ακέραιοι αριθμοί
Οι Φυσικοί αριθμοί περιέχονται στους ακεραίους αριθμούς | |
Αλγεβρική παράστασηΜια παράσταση που περιέχει πράξεις με αριθμούς και μεταβλητές ονομάζεται αλγεβρική παράσταση. Όταν γράφουμε αλγεβρικές παραστάσεις, συνήθως δε βάζουμε το σύμβολο (·) του πολλαπλασιασμού μεταξύ των αριθμών και των μεταβλητών ή μεταξύ των μεταβλητών. Έτσι η προηγούμενη παράσταση γράφεται 2x- 5x+5. Oι προσθετέοι 2x & 5x & 5 λέγονται όροι αυτής. Απλοποιούμε τη μορφή των παραστάσεων κάνοντας Αναγωγή ομοίων όρων . | |
Αναγωγή ομοίων όρωνΗ διαδικασία αυτή με την οποία γράφουμε σε απλούστερη μορφή αλγεβρικές παραστάσεις, ονομάζεται «αναγωγή ομοίων όρων». Βασίζεται στην Eπιμεριστική ιδιότητα. 7 · α + 8 · α = (7 + 8) · α = 15 · α | |
ΑνισότηταΣύγκρισηΓια να συγκρίνουμε λοιπόν δύο πραγματικούς αριθμούς α και β, που δεν έχουν παρασταθεί με σημεία ενός άξονα, βρίσκουμε τη διαφορά τους α - β και εξετάζουμε αν είναι θετική ή αρνητική ή μηδέν. Αν α - β > 0 τότε α > β Διάταξη
Δύο ή περισσότεροι πραγματικοί αριθμοί που έχουν παρασταθεί με σημεία ενός άξονα είναι διατεταγμένοι. Άρα: Κάθε θετικός αριθμός είναι μεγαλύτερος από το μηδέν. Ιδιότητες ανισότητας- διάταξης
Αν α > β και γ > 0 τότε α γ > β γ και $$ \frac{ \alpha }{ \gamma } > \frac{ \beta }{ \gamma } $$. Αν πολλαπλασιάσουμε ή διαιρέσουμε και τα δύο μέλη μιας ανισότητας με τον ίδιο θετικό αριθμό, τότε προκύπτει ανισότητα με την ίδια φορά. Αν α > β και γ < 0 τότε α γ < β γ και $$ \frac{ \alpha }{ \gamma } < \frac{ \beta }{ \gamma } $$. Αν πολλαπλασιάσουμε ή διαιρέσουμε και τα δύο μέλη μιας ανισότητας με τον ίδιο αρνητικό αριθμό, τότε προκύπτει ανισότητα αντίθετης φοράς Αν α > β και γ > δ τότε α + γ > β + δ. Αν προσθέσουμε κατά μέλη δύο ή περισσότερες ανισότητες που έχουν την ίδια φορά, τότε προκύπτει ανισότητα με την ίδια φορά.. Αν α, β, γ, δ θετικοί αριθμοί με α > β και γ > δ τότε αγ > βδ. Αν πολλαπλασιάσουμε κατά μέλη δύο ή περισσότερες ανισότητες που έχουν την ίδια φορά και θετικά μέλη, τότε προκύπτει ανισότητα με την ίδια φορά. α2 ≥ 0. Το τετράγωνο κάθε πραγματικού αριθμού α είναι μη αρνητικός αριθμός. Αν για τους πραγματικούς αριθμούς α, β ισχύει α2 + β2 = 0, τότε α = 0 και β = 0. Αν α > β και β > γ τότε α > γ. Μεταβατική ιδιότητα. Δείτε παράδειγμα ασκήσεων με ανισώσεις ... εδώ.
| |
Αριθμητική παράστασηονομάζεται μια παράσταση που περιέχει πράξεις με αριθμούς.. | |
Αρνητικοί αριθμοίΟι αρνητικοί αριθμοί με πρόσημο - , είναι οι συμμετρικοί των θετικών αριθμών, με πρόσημο + (το οποίο παραλείπεται όταν δε δημιουργείται ασάφεια.
Παράσταση των ρητών αριθμών με σημεία μιας ευθείαςΑν θεωρήσουμε αριστερά της αρχής Ο του ημιάξονα Οx των αριθμών, τον αντικείμενο αυτού ημιάξονα Οx', θα έχουμε τη δυνατότητα, με αυτόν τον τρόπο, να παραστήσουμε όλους τους ρητούς αριθμούς. Το σημείο Α έχει τετμημένη 4 και το σημείο Β έχει τετμημένη -2. Πράξεις με αρνητικούς αριθμούςΠρόσθεση
Αφαίρεση
Πολλαπλασιασμός
Διαίρεση
| |
Ά |
|---|
Άρρητοι αριθμοί
| |
Δ |
|---|
ΔιάνυσμαΟρισμοί
Διανύσματα που έχουν την ίδια διεύθυνση. Ομόρροπα - Αντίρροπα, Ίσα - Αντίθετα
Δύο διανύσματα λέγονται ίσα, όταν έχουν την ίδια διεύθυνση, την ίδια φορά και ίσα μέτρα.
Αντίρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και αντίθετη φορά (αντίθετη κατεύθυνση) Δύο διανύσματα είναι αντίθετα, όταν έχουν την ίδια διεύθυνση, ίσα μέτρα και αντίθετη φορά. ΠΡΟΣΟΧΗ: (Τα διανύσματα $$\overrightarrow {{\rm A}{\rm B}} $$ και $$\overrightarrow {{\rm B}{\rm A}} $$ είναι αντίθετα $$\overrightarrow {{\rm A}{\rm B}} = - \overrightarrow {{\rm B}{\rm A}} $$. Έχουν την ίδια διεύθυνση, αντίθετες φορές και ίσα μέτρα $$\left| {\overrightarrow {{\rm A}{\rm B}} } \right| = \left| {\overrightarrow {{\rm B}{\rm A}} } \right|$$). Πρόσθεση διανυσμάτωνΚανόνας παραλληλογράμμου
Κανόνας πολυγώνου
Στο σχήμα ισχύει ότι $$\overrightarrow \alpha + \overrightarrow \beta + \overrightarrow \gamma = \overrightarrow \delta $$.
Αφαίρεση διανυσμάτων
Μηδενικό διάνυσμαΤο μηδενικό διάνυσμα είναι ένα διάνυσμα του οποίου η αρχή και το τέλος (πέρας) ταυτίζονται. Το μηδενικό διάνυσμα συμβολίζεται με $$\overrightarrow 0 $$. Κάθετα διανύσματα. Σύνθεση - Ανάλυση Ουσιαστικά αντικαθιστούμε τα δυο διανύσματα $$\overrightarrow \alpha $$, $$\overrightarrow \beta $$ με ένα $$\overrightarrow \gamma $$ ώστε $$\overrightarrow \alpha + \overrightarrow \beta = \overrightarrow \gamma $$.
Ανάλυση διανύσματος σε δυο συνιστώσες. Αντικαθιστούμε ένα διάνυσμα $$\overrightarrow \gamma $$ με δυο κάθετες συνιστώσες $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$, που έχουν το αρχικό διάνυσμα ως άθροισμα. Χρησιμοποιούνται οι Τριγωνομετρικοί αριθμοί και προκύπτει ότι:
| |
ΔύναμηΔυνάμεις ρητών αριθμών με φυσικό εκθέτη
Πρόσημο δύναμης
Δυνάμεις ρητών αριθμών με ακέραιο εκθέτη
$$\left( \frac{ \alpha }{ \beta } \right)^{-\ ν}$$=$$\left( \frac{ \beta }{ \alpha } \right)^{\ ν}$$ , $$\left( \frac{ 2 }{ 3 } \right)^{-\ 5}$$=$$\left( \frac{ 3 }{ 2 } \right)^{\ 5}$$
Ιδιότητες δυνάμεων
32 · 33 = 35, 32 · 3- 3 = 3- 1 = $$ \frac{1}{3} $$
32 : 33 = 3-1 = $$ \frac{1}{3} $$, 32 : 3- 3 = 32 - (-3) = 35
(2 · 3)5 = 25 · 35, 25 · 35 = (2 · 3)5 = 65
$$ \frac{4}{25} = \frac{2^{2}}{5^{2}} =\left( \frac{2}{5} \right)^{2}$$
$$4^{3}=\left(2^{2}\right)^{3}=2^{6}$$ | |
Ε |
|---|
Ε.Κ.Π.Ε.Κ.Π. ακεραίων αλγεβρικών παραστάσεωνΕλάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) δύο ή περισσοτέρων ακέραιων αλγεβρικών παραστάσεων που έχουν αναλυθεί σε γινόμενο πρώτων παραγόντων ονομάζεται, το γινόμενο των κοινών και μη κοινών παραγόντων τους με εκθέτη καθενός το μεγαλύτερο από τους εκθέτες του. Παράδειγμα Ε.Κ.Π. (6(x2 - y2), 4(x2 - 2χy + y2), 12(x - y)3} = ? Αναλύουμε τις παραστάσεις και τους συντελεστές τους σε γινόμενα πρώτων παραγόντων: $$6\left( {{x^2} - {y^2}} \right) = 2 \cdot 3(x - y)(x + y)$$ $$12{(x - y)^3} = {2^2} \cdot 3{(x - y)^3}$$ $$4({x^2} - 2xy + {y^2}) = {2^2}{(x - y)^2}$$ $${\rm E}.{\rm K}.\Pi .\left( {2 \cdot 3(x - y)(x + y){{,2}^2}{{(x - y)}^2},\,\,{2^2} \cdot 3{{(x - y)}^3}} \right) = {2^2} \cdot 3(x + y){(x - y)^3} = 12(x + y){(x - y)^3}$$
| |
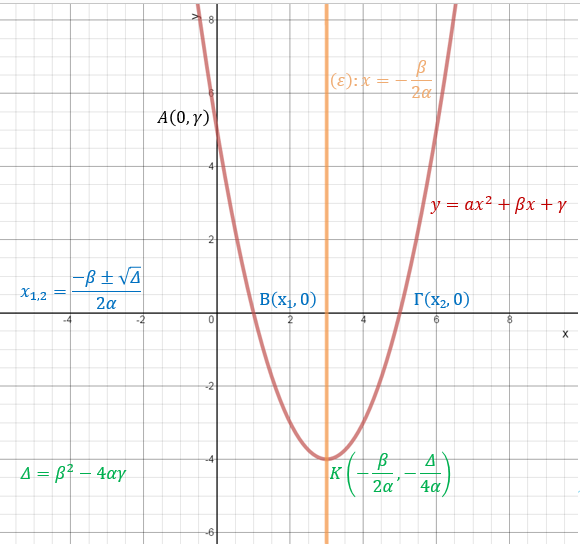
ΕξίσωσηΟνομάζουμε εξίσωση την ισότητα δύο αλγεβρικών παραστάσεων που περιέχουν τουλάχιστον μια μεταβλητή που ονομάζεται άγνωστος.
Εξίσωση πρώτου βαθμούΈχει τη μορφή $$\beta x + \gamma = 0$$.
Αν $$\beta \ne 0$$, τότε; η εξίσωση $$\beta x + \gamma = 0$$ έχει μοναδική λύση την $$x = - \frac{\gamma }{\beta }$$.
Δες σε παράδειγμα τον αλγόριθμο επίλυσης εξίσωσης πρώτου βαθμού ... εδώ. Δες σε παράδειγμα τη διαδικασία επίλυσης προβλήματος με τη χρήση εξίσωσης πρώτου βαθμού ... εδώ.
Εξίσωση δευτέρου βαβμούΣτην εξίσωση $$\alpha {x^2} + \beta x + \gamma = 0$$, η Διακρίνουσα $$\Delta = \sqrt {{\beta ^2} - 4a\gamma } $$ καθορίζει τις ρίζες της εξίσωσης:
Δες αναλυτικά τη θεωρία για την εξίσωση δευτέρου βαθμού ... εδώ.
Παραγοντοποίηση και εξισώσειςΗ παραγοντοποίηση οδηγεί σε παραστάσεις που περιέχουν μόνο γινόμενα $${\rm A} \cdot {\rm B} \cdot \Gamma ...$$. Έτσι η εξίσωση $${\rm A} \cdot {\rm B} \cdot \Gamma ... = 0$$ έχει τις λύσεις: $${\rm A} = 0$$ ή $${\rm B} = 0$$ ή $$\Gamma = 0$$ $$...$$ $${x^2} - 49 = 0 \to {x^2} - {7^2} = 0 \to (x - 7)(x + 7) = 0 \to x - 7 = 0$$ ή $$x + 7 = 0$$ $$ \to $$ $$x = 7$$ ή $$x = - 7$$
Κλασματική εξίσωσηΗ εξίσωση, που περιέχει ένα τουλάχιστον κλάσμα με άγνωστο στον παρονομαστή και η οποία ονομάζεται κλασματική εξίσωση. $$ \frac{4}{x+2} + \frac{4}{x} = \frac{x+8}{x^{2}} $$ Για να ορίζονται οι όροι μιας κλασματικής εξίσωσης πρέπει όλοι οι παρονομαστές να είναι διάφοροι του μηδενός. Στην προηγούμενη εξίσωση πρέπει $$x \neq 0$$ και $$x \neq -2$$ Στις κλασματικές εξισώσεις που περιέχουν σύνθετα κλάσματα πρέπει όλοι οι εμφανιζόμενοι παρονομαστές να είναι διάφοροι του μηδενός. Στην εξίσωση $$ \frac{1}{1+ \frac{1}{x} } =5$$ πρέπει $$x \neq 0$$ και $$x \neq -1$$ ( $$ \frac{1}{1+ \frac{1}{x} } = \frac{1}{ \frac{x+1}{x} } = \frac{x}{x+1} $$) Δες παράδειγμα με την αναλυτική λύση κλασματκής εξίσωσης.... εδώ. Δες παράδειγμα επίλυσης προβλήματος με χρήση κλασματκής εξίσωσης.... εδώ. | |
Ι |
|---|
ΙδιότηταΙδιότητες των πράξεωνΟυδέτερο στοιχείο
Καταστροφικό στοιχείο
Απαγορεύεται
Αντίθετοι αριθμοί
Αντίστροφοι αριθμοί
Αντιμεταθετική ιδιότητα
Προσεταιριστική ιδιότητα
Επιμεριστική ιδιότητα του πολλαπλασιασμού ως προς
| |
ΙσότηταΙδιότητες ισότηταςΧρήσιμες ιδιότητες πράξεων | |
Μ |
|---|
Μ.Κ.Δ.Μ.Κ.Δ. ακεραίων αλγεβρικών παραστάσεωνΜέγιστος Κοινός Διαιρέτης ( Μ.Κ.Δ. ) δύο ή περισσοτέρων ακεραίων αλγεβρικών παραστάσεων που έχουν αναλυθεί σε γινόμενο πρώτων παραγόντων ονομάζεται, το γινόμενο των κοινών παραγόντων τους με εκθέτη καθενός το μικρότερο από τους εκθέτες του. Παράδειγμα Μ.Κ.Δ. (6(x2 - y2), 4(x2 - 2χy + y2), 12(x - y)3} = ? Αναλύουμε τις παραστάσεις και τους συντελεστές τους σε γινόμενα πρώτων παραγόντων: $$6\left( {{x^2} - {y^2}} \right) = 2 \cdot 3(x - y)(x + y)$$ $$12{(x - y)^3} = {2^2} \cdot 3{(x - y)^3}$$ $$4({x^2} - 2xy + {y^2}) = {2^2}{(x - y)^2}$$ $${\rm M}.{\rm K}.\Delta .\left( {2 \cdot 3(x - y)(x + y){{,2}^2}{{(x - y)}^2},\,\,{2^2} \cdot 3{{(x - y)}^3}} \right) = 2(x - y)$$
| |
Μεταβλητήλέγεται ένα γράμμα π.χ x,y,z,ω,…( ελληνικό ή λατινικό) που παριστάνει έναν οποιοδήποτε αριθμό. Χρησιμοποιώντας μεταβλητές "μεταφράζουμε" μια φράση σε Αλγεβρική παράσταση. Παράδειγμα: Το άθροισμα δύο αριθμών πολλαπλασιασμένο επί 9. Αν συμβολίσουμε τους αριθμούς x και y τότε το άθροισμά τους είναι x+y και η ζητούμενη αλγεβρική παράσταση 9(x+y).
| |
ΜονώνυμοΜια Ακέραια αλγεβρική παράσταση λέγεται Μονώνυμο, όταν μεταξύ των μεταβλητών της
Για παράδειγμα οι παραστάσεις $$ - 2{x^2}y,\,\,(3 - \sqrt 2 )x{y^3}\,$$ είναι μονώνυμα ενώ οι $$ - 2{x^2}\sqrt y ,\,\,3 - \sqrt 2 x{y^3},\,\,\frac{x}{y}$$ δεν είναι. Ορολογία
.
Πράξεις μονωνύμωνΤο άθροισμα ομοίων μονωνύμων είναι μονώνυμο όμοιο με αυτά και έχει συντελεστή το άθροισμα των συντελεστών τους (Αναγωγή ομοίων όρων). $$2\sqrt 3 {x^2}y - \,\,(2 - \sqrt 3 ){x^2}y - \,\,{x^2}y = $$ Το γινόμενο μονωνύμων είναι μονώνυμο με:
$$2\sqrt 3 {x^2}y\omega \cdot \,( - \frac{1}{6})x{y^2} = $$ Για να διαιρέσουμε μονώνυμα πολλαπλασιάζουμε τον διαιρετέο με τον αντίστροφο του διαιρέτη. $$2\sqrt 3 {x^2}y:\,\left[ {( - \frac{1}{6})x{y^2}\omega } \right] = $$ $$2\sqrt 3 {x^2}y \cdot \,\frac{1}{{( - \frac{1}{6})x{y^2}\omega }} = $$ $$\frac{{2\sqrt 3 }}{{( - \frac{1}{6})}} \cdot \frac{{{x^2}}}{x} \cdot \,\frac{y}{{{y^2}}} \cdot \frac{1}{\omega } = $$ $$ - 12\sqrt {3 \cdot } {x^{2 - 1}} \cdot {y^{1 - 2}} \cdot {\omega ^{ - 1}} = $$ $$\frac{{ - 12\sqrt 3 x}}{{y\omega }}$$ Στη διαίρεση μονωνύμων μπορεί να προκύψει μονώνυμο μικρότερου βαθμού ($$5{x^2}y:\,\,({x^{}}y) = 5x$$), σταθερό μονώνυμο ($$5{x^2}y:\,\,({x^2}y) = 5$$) ή μη ακέραια αλγεβρική παράσταση όπως στο παράδειγμα. | |
Π |
|---|
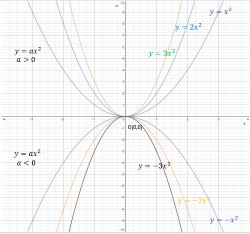
Παραβολή
| |
ΠαραγοντοποίησηΗ διαδικασία με την οποία μια παράσταση, που είναι άθροισμα, μετατρέπεται σε γινόμενο παραγόντων, λέγεται παραγοντοποίηση. Αξιοσημείωτες παραγοντοποιήσειςΠαράσταση δύο όρωνΔιαφορά τετραγώνων: $${\rm{ }}{\alpha ^2} - {\rm{ }}{\beta ^2} = \left( {\alpha {\rm{ + }}\beta } \right)\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)$$$$4{\beta ^2} - 25 = {\left( {2\beta } \right)^{}} - {5^2} = \left( {2\beta + 5} \right)\left( {2\beta - 5} \right)$$ $${\alpha ^6} - {\beta ^6} = {\left( {{\alpha ^3}} \right)^2} - {\left( {{\beta ^3}} \right)^2} = \left( {{\alpha ^3} + {\beta ^3}} \right)\left( {{\alpha ^3} - {\beta ^3}} \right) = \left( {\alpha {\rm{ + }}\beta } \right)\left( {{\alpha ^2}{\rm{ - }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right)\left( {\alpha {\rm{ + }}\beta } \right)\left( {{\alpha ^2}{\rm{ - }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right)$$ $${2014^2} - {1986^2} = (2000 + 14)(2000 - 14) = {2000^2} - {14^2} = 4.000.000 - 196 = 3.999.804$$ Διαφορά κύβων: $${\alpha ^3} - {\rm{ }}{\beta ^3} = \left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)\left( {{\alpha ^2} + {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }}$$$${{\rm{x}}^{\rm{3}}} - 27 = {{\rm{x}}^{\rm{3}}} - {9^3} = \left( {x - 3} \right)\left( {{x^2} - 3x + {3^2}} \right) = \left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right)$$ $${\alpha ^6} - {\beta ^6} = {\left( {{\alpha ^2}} \right)^3} - {\left( {{\beta ^2}} \right)^3} = \left( {{\alpha ^2} - {\beta ^2}} \right)\left[ {{{\left( {{\alpha ^2}} \right)}^2} + {\alpha ^2}{\beta ^2} + {{\left( {{\beta ^2}} \right)}^2}} \right] = \left( {{\alpha ^2} - {\beta ^2}} \right)\left[ {{\alpha ^4} + {\alpha ^2}{\beta ^2} + {\beta ^4}} \right]$$ Άθροισμα κύβων: $${\alpha ^3} - {\rm{ }}{\beta ^3} = \left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)\left( {{\alpha ^2} + {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }}$$$${\alpha ^6} + {\beta ^6} = {\left( {{\alpha ^2}} \right)^3} + {\left( {{\beta ^2}} \right)^3} = \left( {{\alpha ^2} + {\beta ^2}} \right)\left[ {{{\left( {{\alpha ^2}} \right)}^2} - {\alpha ^2}{\beta ^2} + {{\left( {{\beta ^2}} \right)}^2}} \right] = \left( {{\alpha ^2} + {\beta ^2}} \right)\left[ {{\alpha ^4} - {\alpha ^2}{\beta ^2} + {\beta ^4}} \right]$$ Κοινός παράγοντας$${x^5} - x = x\left( {{x^4} - 1} \right) = x\left[ {{{\left( {{x^2}} \right)}^2} - {1^2}} \right] = x\left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right) = x\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)$$ Παράσταση τριών όρωνΤέλειο τετράγωνο αθροίσματος ή διαφοράς: $${\alpha ^2} \pm {\rm{ }}2\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2} = {\left( {\alpha {\rm{ }} \pm {\rm{ }}\beta } \right)^2}$$$${y^4} - {\rm{ }}2{y^2} + {\rm{ }}1 = {\left( {{y^2}} \right)^2} - 2 \cdot \left( {{y^2}} \right) \cdot 1 = {\left( {{y^2} - 1} \right)^2}$$ $$25{\rm{ + }}10{x^3} + {\rm{ }}{x^6} = {5^2} + 2 \cdot 5 \cdot {x^3} + {\left( {{x^3}} \right)^2} = {\left( {5 + {x^3}} \right)^2}$$ Τριώνυμο της μορφής $${x^2} + (\alpha + \beta )x + \alpha \beta $$: $${x^2} + (\alpha + \beta )x + \alpha \beta = (x + \alpha )(x + \beta )$$$${x^2} + {\rm{ }}8x{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}{x^2} + {\rm{ }}\left( {6{\rm{ }} + {\rm{ }}2} \right)x{\rm{ }} + {\rm{ }}6 \cdot 2{\rm{ }} = {\rm{ }}\left( {x{\rm{ }} + {\rm{ }}6} \right)\left( {x{\rm{ }} + {\rm{ }}2} \right)$$ $${x^2} - 5x + 6 = {\rm{ }}{x^2} + \left( { - 3 - 2} \right)x{\rm{ }} + {\rm{ }}( - 3) \cdot ( - 2){\rm{ }} = {\rm{ }}\left( {x - 3} \right)\left( {x - 2{\rm{ }}} \right)$$ Τριώνυμο της μορφής $$\alpha {x^2} + \beta x + \gamma = 0$$ = $$a(x - {\rho _1})(x - {\rho _2})$$ με $${\rho _{1,2}} = \frac{{ - \beta \pm \sqrt {{b^2} - 4a\gamma } }}{{2a}}$$$$2{x^2} + 5x + 3$$. Η εξίσωση $$2{x^2} + 5x + 3 = 0$$ έχει δυο λύσεις, $${\rho _{1,2}} = \frac{{ - 5 \pm \sqrt {{5^2} - 4 \cdot 2 \cdot 3} }}{2}$$, τις $${\rho _1} = - 1$$ και $${\rho _1} = - \frac{3}{2}$$ Έτσι το τριώνυμο γίνεται: $$2{x^2} + 5x + 3 = 2\left[ {x - ( - 1)} \right]\left[ {x - \left( { - \frac{3}{2}} \right)} \right] = 2(x + 1)\left( {x + \frac{3}{2}} \right)$$ Κοινός παράγοντας$$ - 4{y^2} + 4y - 1 = - (4{y^2} - 4y + 1) = - \left[ {{{\left( {2y} \right)}^2} - 2 \cdot \left( {2y} \right) + {1^2}} \right] = - {\left( {2y - 1} \right)^2}$$ $$3{x^3} + 12{x^2} - 15x = 3x({x^2} + 4x - 5) = 3x\left[ {{x^2} + (5 - 1)x + ( - 1) \cdot ( + 5)} \right] = 3x(x + 5)(x - 1)$$ Παράσταση τεσσάρων όρωνΤέλειος κύβος αθροίσματος ή διαφοράς: $${\alpha ^3} \pm 3{\alpha ^2}\beta + 3\alpha {\beta ^2} \pm {\beta ^3} = {(\alpha \pm \beta )^3}$$$$1 - 4y + 8{y^2} - 8{y^3} = {1^3} - 2 \cdot {1^2} \cdot (2y) + 2 \cdot 1 \cdot {(2y)^2} - {(2y)^3} = {(1 - 2y)^3}$$ Ομαδοποίηση 3-1$${x^2} - 2x + 1 - {y^2} = ({x^2} - 2 \cdot x \cdot 1 + {1^2}) - {y^2} = {(x - 1)^2} - {y^2} = (x - 1 - y)(x - 1 + y)$$ Ομαδοποίηση 2-2$$9{x^3} + 9{x^2} - 4x - 4 = 9{x^2}(x + 1) - 4(x + 1) = (x + 1)(9{x^2} - 4) = (x + 1)\left[ {{{(3x)}^2} - {2^2}} \right] = (x + 1)(3x + 2)(3x - 2)$$ Διάσπαση ενός εκ των τριών όρων και δημιουργία τέταρτου$$3{x^2} + 5xy + 2{y^2} = 3{x^2} + 3xy + 2xy + 2{y^2} = 3x(x + y) + 2y(x + y) = (x + y)(3x + 2y)$$ $${\alpha ^4} + {\beta ^4} - 7{\alpha ^2}{\beta ^2} = {\alpha ^4} + {\beta ^4} + 2{\alpha ^2}{\beta ^2} - 9{\alpha ^2}{\beta ^2} = {\left( {{\alpha ^2}} \right)^2} + {\left( {{\beta ^2}} \right)^2} + 2{\alpha ^2}{\beta ^2} - {\left( {3\alpha \beta } \right)^2} = {\left( {{\alpha ^2} + {\beta ^2}} \right)^2} - {\left( {3\alpha \beta } \right)^2} = \left( {{\alpha ^2} + {\beta ^2} - 3\alpha \beta } \right)\left( {{\alpha ^2} + {\beta ^2} + 3\alpha \beta } \right)$$ Παραγοντοποίηση και εξισώσειςΗ παραγοντοποίηση οδηγεί σε παραστάσεις που περιέχουν μόνο γινόμενα $${\rm A} \cdot {\rm B} \cdot \Gamma ...$$. Έτσι η εξίσωση $${\rm A} \cdot {\rm B} \cdot \Gamma ... = 0$$ έχει τις λύσεις: $${\rm A} = 0$$ ή $${\rm B} = 0$$ ή $$\Gamma = 0$$ $$...$$ $${x^2} - 49 = 0 \to {x^2} - {7^2} = 0 \to (x - 7)(x + 7) = 0 \to x - 7 = 0$$ ή $$x + 7 = 0$$ $$ \to $$ $$x = 7$$ ή $$x = - 7$$ | |
ΠολυώνυμοΜια αλγεβρική παράσταση λέγεται Πολυώνυμο, όταν μεταξύ των μεταβλητών της
Για παράδειγμα η παράσταση $$2{x^2}y + 3{x^2}y - x{y^2} - 2x{y^2}$$ είναι το πολυώνυμο $$5{x^2}y - 3x{y^2}$$. Ορολογία
.
Πράξεις πολυωνύμωνΜπορούμε να προσθέσουμε, να αφαιρέσουμε, ή να πολλαπλασιάσουμε πολυώνυμα, χρησιμοποιώντας τις ιδιότητες των πραγματικών αριθμών, όπως φαίνεται στα επόμενα παραδείγματα: Πρόσθεση (x3 + 2x2 - 5x + 7) + (4x3 - 5x2 + 3) = = x3 + 2x2 - 5x + 7 + 4x3 - 5x2 + 3 = = (1 + 4)x3 + (2 - 5)x2 - 5x + (7 + 3) = = 5x3 - 3x2 - 5x + 10 [Πολυώνυμο 3ου βαθμού]
(2x3 - x2 + 1) + (-2x3 + 2x - 3) = = 2x3 - x2 + 1 - 2x3 + 2x - 3 = = -x2 + 2x - 2 [Πολυώνυμο 2ου βαθμού]
(x3 - 3x2 - 1) + (-x3 + 3x2 + 1) = = x3 - 3x2 - 1 - x3 + 3x2 + 1 = 0 [Μηδενικό πολυώνυμο]
Αφαίρεση (x3 + 2x2 - 5x + 7) - (4x3 - 5x2 + 3) = x3 + 2 x2 - 5x + 7 - 4x3 + 5x2 - 3 = -3x3 + 7x2 - 5x + 4 [Πολυώνυμο 3ου βαθμού]
Πολλαλασιασμός
(x2 + 5x)(2x3 + 3x - 1) =
= x2(2x3 + 3x - 1) + 5x(2x3 + 3x - 1) = 2x5 + 3x3 - x2 + 10x4 + 15x2 - 5x = 2x5 + 10x4 + 3x3 + 14x2 - 5x [Πολυώνυμο 5ου βαθμού] Για το βαθμό του αθροίσματος και του γινομένου δυο πολυωνύμων ισχύει ότι:
Διαίρεση
Δείτε παραδείγματα διαίρεσης
| |
Πραγματικοί αριθμοίΟι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς Άξονας πραγματικών αριθμών
Οι ακέραιοι αριθμοί: ... -3, -2, -1, 0, 1, 2, 3 ... παριστάνονται πάλι με σημεία. Το σύνολο των ρητών αριθμών, δηλαδή των αριθμών που μπορούν να γραφούν στη μορφή, όπου μ ακέραιος και ν φυσικός αριθμός. Οι ρητοί αριθμοί έχουν γνωστή δεκαδική μορφή και γεμίζουν την ευθεία, αλλά όχι πλήρως. Οι πραγματικοί αριθμοί αποτελούνται όχι μόνο από τους ρητούς αλλά και όλους τους άρρητους.
| |
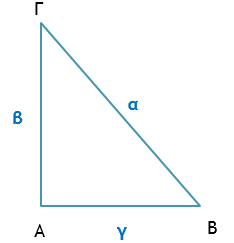
Πυθαγόρειο θεώρημα
ΒΓ2 = ΑΒ2 + ΑΓ2α2 = β2 + γ2
Αντίστροφο Πυθαγόρειο θεώρημα Αν ισχύει η σχέση ΚΛ2 = ΜΛ2 + ΜΚ2 μεταξύ των πλευρών ενός τριγώνου ΚΛΜ , τότε το τρίγωνο είναι ορθογώνιο με ορθή γωνία τη γωνία Μ. | |
Ρ |
|---|
Ρητή αλγεβρική παράστασηΜια αλγεβρική παράσταση που είναι κλάσμα με όρους πολυώνυμα, λέγεται ρητή αλγεβρικήπαράσταση ή απλώς ρητή παράσταση. π.χ. $$A = \frac{{3{x^2} + 12x + 12}}{{{x^2} - 4}}$$ Οι μεταβλητές μιας ρητής παράστασης δεν μπορούν να πάρουν τιμές που μηδενίζουν τον παρονομαστή. $${x^2} - 4 \ne 0$$ ή $${x^2} \ne 4$$ ή $$x \ne \sqrt 4 $$ ή $$x \ne \pm 2$$. Η μεταβλητή x μπορεί να έχει ως τιμή κάθε πραγματικό αριθμός εκτός των -2, +2. Για να απλοποιήσουμε μια ρητή αλγεβρική παράσταση, παραγοντοποιούμε και τους δύο όρους της και διαγράφουμε τον κοινό παράγοντα. $$A = \frac{{3{x^2} + 12x + 12}}{{{x^2} - 4}} = \frac{{3\left( {{x^2} + 4x + 4} \right)}}{{{x^2} - 4}} = \frac{{3\left( {{x^2} + 2 \cdot 2 \cdot x + {2^2}} \right)}}{{{x^2} - {2^2}}} = \frac{{3{{(x + 2)}^2}}}{{(x - 2)(x + 2)}} = \frac{{3(x + 2)}}{{x - 2}}$$ Οι πράξεις με τις ρητές παραστάσεις γίνονται όπως και οι πράξεις των αριθμητικών κλασμάτων. | |
Ρητοί αριθμοί
Μορφή ρητού αριθμού: $$ \frac{ \mu }{ \nu } $$ με ν ≠ 0 κια Μ.Κ.Δ. (μ,ν) =1 Κάθε ρητός αριθμός μπορεί να γραφεί και σε δεκαδική μορφή. Αυτό γίνεται κάνοντας τη διαίρεση μ / ν. Η διαίρεση αυτή μπορεί
Οι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς
| |
Τ |
|---|
ΤαυτότηταΤαυτότητα λέγεται κάθε ισότητα που περιέχει μεταβλητές και αληθεύει για όλες τις τιμές των μεταβλητών της. Αξιοσημείωτες ταυτότητεςΤο δεύτερα μέλη των ταυτοτήτων που ακολουθούν ονομάζονται αναπτύγματα. Τετράγωνο αθροίσματος$${\left( {\alpha {\rm{ }} + {\rm{ }}\beta } \right)^2} = {\rm{ }}{\alpha ^2} + {\rm{ }}2\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}$$ $${\left( {y{\rm{ }} + {\rm{ }}4} \right)^2} = {\rm{ }}{y^2} + {\rm{ }}2 \cdot y \cdot 4{\rm{ }} + {\rm{ }}{4^2} = {\rm{ }}{y^2} + {\rm{ }}8y{\rm{ }} + {\rm{ }}16$$ $${\left( {\sqrt 3 + 1} \right)^2} = {\left( {\sqrt 3 } \right)^2} + {\rm{ }}2 \cdot \sqrt 3 \cdot 1{\rm{ }} + {\rm{ }}{{\rm{1}}^2} = {\rm{ }}3 + {\rm{ }}2\sqrt 3 {\rm{ }} + {\rm{ }}1 = 4 + 2\sqrt 3 {\rm{ }}$$
Τετράγωνο διαφοράς$${\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)^2} = {\rm{ }}{\alpha ^2} - {\rm{ }}2\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}$$ $${\left( {\omega - \frac{2}{\omega }} \right)^2} = {\omega ^2} - 2 \cdot \omega \cdot \frac{2}{\omega } + {\left( {\frac{2}{\omega }} \right)^2} = {\omega ^2} - 4 + \frac{4}{{{\omega ^2}}}$$ $${\left( {1 - \sqrt 7 } \right)^2} = 1 - 2 \cdot 1 \cdot \sqrt 7 + {\left( {\sqrt 7 } \right)^2} = {\rm{ }}3 - {\rm{ }}2\sqrt 7 {\rm{ }} + {\rm{ 7}} = 10 - 2\sqrt 7 {\rm{ }}$$
Κύβος αθροίσματος$${\left( {\alpha {\rm{ }} + {\rm{ }}\beta } \right)^3} = {\rm{ }}{\alpha ^3} + {\rm{ }}3{\alpha ^2}\beta + 3\alpha {\beta ^2} + {\beta ^3}$$ $${\left( {{\rm{2x }} + {\rm{ 1}}} \right)^3} = {\rm{ }}{\left( {2x} \right)^3} + {\rm{ }}3 \cdot {\left( {2x} \right)^2} \cdot 1 + 3 \cdot \left( {2x} \right) \cdot {1^2} + {1^3} = 8{x^3} + 12{x^2} + 6x + 1$$ $${\left( {\sqrt {\rm{2}} {\rm{ }} + {\rm{ 1}}} \right)^3} = {\rm{ }}{\left( {\sqrt {\rm{2}} } \right)^3} + {\rm{ }}3 \cdot {\left( {\sqrt {\rm{2}} } \right)^2} \cdot 1 + 3 \cdot \left( {\sqrt {\rm{2}} } \right) \cdot {1^2} + {1^3} = {\left( {\sqrt {\rm{2}} } \right)^2} \cdot \sqrt {\rm{2}} + 3 \cdot 2 \cdot 1 + 3\sqrt 2 + 1 = 2\sqrt {\rm{2}} + 6 + 3\sqrt 2 + 1 = 5\sqrt {\rm{2}} + 7$$
Κύβος διαφοράς$${\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)^3} = {\rm{ }}{\alpha ^3} - {\rm{ }}3{\alpha ^2}\beta + 3\alpha {\beta ^2} - {\beta ^3}$$ $${\left( {{\omega ^2} - {\rm{ }}2\omega } \right)^3} = {\left( {{\omega ^2}} \right)^3} - {\rm{ }}3 \cdot {\left( {{\omega ^2}} \right)^2} \cdot \left( {2\omega } \right) + 3 \cdot \left( {{\omega ^2}} \right) \cdot {\left( {2\omega } \right)^2} - {\left( {2\omega } \right)^3} = {\omega ^6} - 3 \cdot \left( {{\omega ^4}} \right) \cdot \left( {2\omega } \right) + 3 \cdot \left( {{\omega ^2}} \right) \cdot \left( {4{\omega ^2}} \right) - 8{\omega ^3} = {\omega ^6} - 6{\omega ^5} + 12{\omega ^4} - 8{\omega ^3}$$ $${\left( {\sqrt {\rm{2}} {\rm{ - }}\sqrt {\rm{3}} } \right)^3} = {\rm{ }}{\left( {\sqrt {\rm{2}} } \right)^3}{\rm{ - }}3 \cdot {\left( {\sqrt {\rm{2}} } \right)^2} \cdot \sqrt {\rm{3}} + 3 \cdot \left( {\sqrt {\rm{2}} } \right) \cdot {\left( {\sqrt {\rm{3}} } \right)^2} - {\left( {\sqrt {\rm{3}} } \right)^3} = {\left( {\sqrt {\rm{2}} } \right)^2} \cdot \sqrt {\rm{2}} - 3 \cdot 2 \cdot \sqrt {\rm{3}} + 3 \cdot \sqrt 2 \cdot 3 - {\left( {\sqrt {\rm{3}} } \right)^2} \cdot \sqrt {\rm{3}} = 2\sqrt {\rm{2}} - 6\sqrt {\rm{3}} + 9\sqrt 2 - 3\sqrt {\rm{3}} = 11\sqrt 2 - 9\sqrt {\rm{3}} $$
Γινόμενο αθροίσματος επί διαφορά$$\left( {\alpha {\rm{ + }}\beta } \right)\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right){\rm{ = }}{\alpha ^2} - {\rm{ }}{\beta ^2}$$ $$\left( {{\alpha ^3}{\rm{ + }}{\beta ^3}} \right)\left( {{\alpha ^3}{\rm{ }} - {\rm{ }}{\beta ^3}} \right){\rm{ = }}{\left( {{\alpha ^3}} \right)^2} - {\rm{ }}{\left( {{\beta ^3}} \right)^2} = {\alpha ^6}{\rm{ }} - {\rm{ }}{\beta ^6}$$ $$99 \cdot 101 = \left( {100 - 1} \right)\left( {100 + 1} \right) = {100^2} - {1^2} = 10000 - 1 = 9999$$
Τα γινόμενα του αθροίσματος ή της διαφοράς κύβων$$\left( {\alpha {\rm{ }} + {\rm{ }}\beta } \right)\left( {{\alpha ^2} - {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }} = {\rm{ }}{\alpha ^3} + {\rm{ }}{\beta ^3}$$ $$\left( {x{\rm{ }} + {\rm{ }}3} \right)\left( {{x^2} - {\rm{ }}3x{\rm{ }} + {\rm{ }}9} \right){\rm{ }} = {\rm{ }}\left( {x{\rm{ }} + {\rm{ }}3} \right)\left( {{x^2} - {\rm{ }}3x{\rm{ }} + {\rm{ }} + {\rm{ }}{3^2}} \right){\rm{ }} = {\rm{ }}{x^3} + {\rm{ }}{3^3} = {\rm{ }}{x^3} + {\rm{ }}27$$ $$\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)\left( {{\alpha ^2} + {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }} = {\rm{ }}{\alpha ^3} - {\rm{ }}{\beta ^3}$$ $$\left( {x{\rm{ }} - {\rm{ }}2} \right)\left( {{x^2} + {\rm{ }}2x{\rm{ }} + {\rm{ }}4} \right){\rm{ }} = {\rm{ }}\left( {x{\rm{ }} - {\rm{ }}2} \right)\left( {{x^2} + {\rm{ }}2x{\rm{ }} + {\rm{ }} + {\rm{ }}{2^2}} \right){\rm{ }} = {\rm{ }}{x^3} - {\rm{ }}{2^3} = {\rm{ }}{x^3}{\rm{ }} - {\rm{ }}8$$ | |
Τετραγωνική ρίζαΤετρ. ρίζα ενός θετικού αριθμού α, λέγεται ο θετικός αριθμός, ο οποίος, όταν υψωθεί στο τετράγωνο, δίνει τον αριθμό α. Η τετρ. ρίζα του α συμβολίζεται με $$ \sqrt{ \alpha } $$.
Ιδιότητες
Προσοχή!
Χρήσιμες ιδιότητες για την απλοποίηση παραστάσεων Ρίζα δύναμης με άρτιο εκθέτη: $$\sqrt {{\alpha ^{2\nu }}} = \sqrt {{{\left( {{\alpha ^\nu }} \right)}^2}} = {\alpha ^\nu }$$
| |
Τριγωνομετρικοί αριθμοίΟρισμοίΓια τις οξείες γωνίες ενός ορθογωνίου τριγώνου δίνονται οι εξής ορισμοί. $${\rm E}\Phi {\rm A}\Pi {\rm T}{\rm O}{\rm M}{\rm E}{\rm N}{\rm H} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}$$ $${\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$ $$\Sigma \Upsilon {\rm N}{\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$
$$\begin{array}{l}\varepsilon \varphi {\rm B} = \frac{{{\rm A}\Gamma }}{{{\rm A}{\rm B}}} = \frac{\beta }{\gamma }\,\,\,\,\,\,\,\,\,\,\,\,\varepsilon \varphi \Gamma = \frac{{{\rm A}{\rm B}}}{{{\rm A}\Gamma }} = \frac{\gamma }{\beta }\\\eta \mu {\rm B} = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\eta \mu \Gamma = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\\\sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\end{array}$$ Γνωρίζουμε ότι σε κάθε ορθογώνιο τρίγωνο η υποτείνουσα είναι μεγαλύτερη από καθεμία από τις κάθετες πλευρές. Επομένως ισχύουν οι ανισώσεις: 0 < ημω < 1 και 0 < συνω < 1
Σχέσεις τριγωνομετρικών αριθμώνΓια κάθε γωνία ισχύει ότι $$\varepsilon \varphi \omega = \frac{{\eta \mu \omega }}{{\sigma \upsilon \nu \omega }}\,\,\,\,\left\{ {\frac{{\eta \mu \Gamma }}{{\sigma \upsilon \nu \Gamma }} = \frac{{\frac{\gamma }{\alpha }}}{{\frac{\beta }{\alpha }}} = \frac{{\gamma \cdot \alpha }}{{\beta \cdot \alpha }} = \frac{\gamma }{\beta } = \varepsilon \varphi \Gamma } \right\}$$ Όπως φαίνεται $$\eta \mu {\rm B} = \sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,$$ και $$\eta \mu \Gamma = \sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }$$, δηλαδή το ημίτονο μιας γωνίας ισούται με το συνημίτονο της συμπληρωματικής της. Παρατηρήστε ότι $$\,\varepsilon \varphi \Gamma = \frac{1}{{\varepsilon \varphi {\rm B}}}$$, δηλαδή οι εφαπτομένες συμπληρωματικών γωνιών είναι αριθμοί αντίστροφοι, έχουν γινόμενο 1 $$\varepsilon \varphi {\rm B} \cdot \varepsilon \varphi \Gamma = \frac{\gamma }{\beta } \cdot \frac{\beta }{\gamma } = 1\,$$. Μεταβολές τριγωνομετρικών αριθμών οξειών γωνιώνΌταν μια οξεία γωνία αυξάνεται↑, τότε: αυξάνεται το ημίτονό↑ της, ελαττώνεται το συνημίτονό↓ της και αυξάνεται η εφαπτομένη↑ της. Χαρακτηριστικές τιμές τριγωνομετρικών αριθμών οξειών γωνιών$$\begin{array}{ccccccccccccccc}{}&{{{30}^o}}&{{{45}^o}}&{{{60}^o}}\\{\eta \mu }&{\frac{1}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 3 }}{2}}\\{\sigma \upsilon \nu }&{\frac{{\sqrt 3 }}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{1}{2}}\\{\varepsilon \varphi }&{\frac{{\sqrt 3 }}{3}}&1&{\sqrt 3 }\end{array}$$ | |
Υ |
|---|
Υπερβολή
Και στις δύο περιπτώσεις η γραφική παράσταση μιας υπερβολής έχει:
Όταν οι μεταβλητές x , y εκφράζουν ποσά / μεγέθη, τότε τα ποσά / μεγέθη αυτά είναι αντιστρόφως ανάλογα, το γινόμενό τους είναι η σταθερά α. Δεἰτε ένα παράδειγμα αντιστρόφως ποσών και τη μελέτη με τη χρήση συναρτήσεων και γραφικών... εδώ. | |
Φ |
|---|
Φυσικοί αριθμοίΟι αριθμοί 0, 1, 2, 3, 4, 5, 6......... 98, 99, 100........ 1999, 2000, 2001, ... ονομάζονται φυσικοί αριθμοί.
Κάθε φυσικός αριθμός έχει έναν επόμενο και ένα προηγούμενο φυσικό αριθμό, εκτός από το 0 που έχει μόνο επόμενο, το 1. Περισσότερα... | |

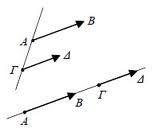 Ομόρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και την ίδια φορά (ἰδια κατεύθυνση)
Ομόρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και την ίδια φορά (ἰδια κατεύθυνση)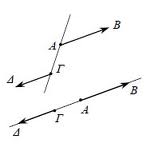
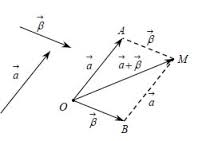 Μεταφέρουμε τα διανύσματα, έτσι ώστε να έχουν κοινή αρχή και σχηματίζουμε το παραλληλόγραμμο που έχει πλευρές τα διανύσματα. Η διαγώνιος του παραλληλογράμμου που έχει ως αρχή την κοινή τους αρχή είναι το άθροισμα των διανυσμάτων.
Μεταφέρουμε τα διανύσματα, έτσι ώστε να έχουν κοινή αρχή και σχηματίζουμε το παραλληλόγραμμο που έχει πλευρές τα διανύσματα. Η διαγώνιος του παραλληλογράμμου που έχει ως αρχή την κοινή τους αρχή είναι το άθροισμα των διανυσμάτων. 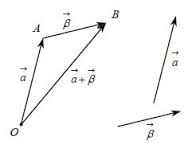
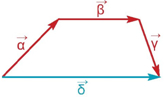 Μεταφέρουμε παράλληλα τα διανύσματα που θέλουμε να προσθέσουμε, ώστε να γίνουν όλα διαδοχικά. Το άθροισμα των θα είναι το
Μεταφέρουμε παράλληλα τα διανύσματα που θέλουμε να προσθέσουμε, ώστε να γίνουν όλα διαδοχικά. Το άθροισμα των θα είναι το 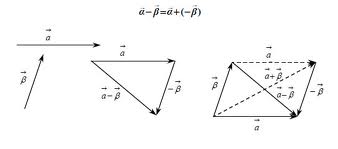 Η διαφορά δύο διανυσμάτων $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$ συμβολίζεται με $$\overrightarrow \alpha - \overrightarrow \beta $$ και ορίζεται ως άθροισμα του $$\overrightarrow \alpha $$ με το αντίθετο
Η διαφορά δύο διανυσμάτων $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$ συμβολίζεται με $$\overrightarrow \alpha - \overrightarrow \beta $$ και ορίζεται ως άθροισμα του $$\overrightarrow \alpha $$ με το αντίθετο 
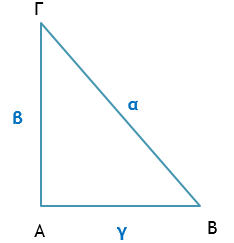 Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.
Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.