Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ
Σελίδα: (Προηγούμενο) 1 2 3 (Επόμενο)
ΟΛΑ
Δ |
|---|
Ε |
|---|
Ε.Κ.Π.Ε.Κ.Π. ακεραίων αλγεβρικών παραστάσεωνΕλάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) δύο ή περισσοτέρων ακέραιων αλγεβρικών παραστάσεων που έχουν αναλυθεί σε γινόμενο πρώτων παραγόντων ονομάζεται, το γινόμενο των κοινών και μη κοινών παραγόντων τους με εκθέτη καθενός το μεγαλύτερο από τους εκθέτες του. Παράδειγμα Ε.Κ.Π. (6(x2 - y2), 4(x2 - 2χy + y2), 12(x - y)3} = ? Αναλύουμε τις παραστάσεις και τους συντελεστές τους σε γινόμενα πρώτων παραγόντων: $$6\left( {{x^2} - {y^2}} \right) = 2 \cdot 3(x - y)(x + y)$$ $$12{(x - y)^3} = {2^2} \cdot 3{(x - y)^3}$$ $$4({x^2} - 2xy + {y^2}) = {2^2}{(x - y)^2}$$ $${\rm E}.{\rm K}.\Pi .\left( {2 \cdot 3(x - y)(x + y){{,2}^2}{{(x - y)}^2},\,\,{2^2} \cdot 3{{(x - y)}^3}} \right) = {2^2} \cdot 3(x + y){(x - y)^3} = 12(x + y){(x - y)^3}$$
| |
ΕξίσωσηΟνομάζουμε εξίσωση την ισότητα δύο αλγεβρικών παραστάσεων που περιέχουν τουλάχιστον μια μεταβλητή που ονομάζεται άγνωστος.
Εξίσωση πρώτου βαθμούΈχει τη μορφή $$\beta x + \gamma = 0$$.
Αν $$\beta \ne 0$$, τότε; η εξίσωση $$\beta x + \gamma = 0$$ έχει μοναδική λύση την $$x = - \frac{\gamma }{\beta }$$.
Δες σε παράδειγμα τον αλγόριθμο επίλυσης εξίσωσης πρώτου βαθμού ... εδώ. Δες σε παράδειγμα τη διαδικασία επίλυσης προβλήματος με τη χρήση εξίσωσης πρώτου βαθμού ... εδώ.
Εξίσωση δευτέρου βαβμούΣτην εξίσωση $$\alpha {x^2} + \beta x + \gamma = 0$$, η Διακρίνουσα $$\Delta = \sqrt {{\beta ^2} - 4a\gamma } $$ καθορίζει τις ρίζες της εξίσωσης:
Δες αναλυτικά τη θεωρία για την εξίσωση δευτέρου βαθμού ... εδώ.
Παραγοντοποίηση και εξισώσειςΗ παραγοντοποίηση οδηγεί σε παραστάσεις που περιέχουν μόνο γινόμενα $${\rm A} \cdot {\rm B} \cdot \Gamma ...$$. Έτσι η εξίσωση $${\rm A} \cdot {\rm B} \cdot \Gamma ... = 0$$ έχει τις λύσεις: $${\rm A} = 0$$ ή $${\rm B} = 0$$ ή $$\Gamma = 0$$ $$...$$ $${x^2} - 49 = 0 \to {x^2} - {7^2} = 0 \to (x - 7)(x + 7) = 0 \to x - 7 = 0$$ ή $$x + 7 = 0$$ $$ \to $$ $$x = 7$$ ή $$x = - 7$$
Κλασματική εξίσωσηΗ εξίσωση, που περιέχει ένα τουλάχιστον κλάσμα με άγνωστο στον παρονομαστή και η οποία ονομάζεται κλασματική εξίσωση. $$ \frac{4}{x+2} + \frac{4}{x} = \frac{x+8}{x^{2}} $$ Για να ορίζονται οι όροι μιας κλασματικής εξίσωσης πρέπει όλοι οι παρονομαστές να είναι διάφοροι του μηδενός. Στην προηγούμενη εξίσωση πρέπει $$x \neq 0$$ και $$x \neq -2$$ Στις κλασματικές εξισώσεις που περιέχουν σύνθετα κλάσματα πρέπει όλοι οι εμφανιζόμενοι παρονομαστές να είναι διάφοροι του μηδενός. Στην εξίσωση $$ \frac{1}{1+ \frac{1}{x} } =5$$ πρέπει $$x \neq 0$$ και $$x \neq -1$$ ( $$ \frac{1}{1+ \frac{1}{x} } = \frac{1}{ \frac{x+1}{x} } = \frac{x}{x+1} $$) Δες παράδειγμα με την αναλυτική λύση κλασματκής εξίσωσης.... εδώ. Δες παράδειγμα επίλυσης προβλήματος με χρήση κλασματκής εξίσωσης.... εδώ. | |
Ι |
|---|
ΙδιότηταΙδιότητες των πράξεωνΟυδέτερο στοιχείο
Καταστροφικό στοιχείο
Απαγορεύεται
Αντίθετοι αριθμοί
Αντίστροφοι αριθμοί
Αντιμεταθετική ιδιότητα
Προσεταιριστική ιδιότητα
Επιμεριστική ιδιότητα του πολλαπλασιασμού ως προς
| |
ΙσότηταΙδιότητες ισότηταςΧρήσιμες ιδιότητες πράξεων | |
Μ |
|---|
Μ.Κ.Δ.Μ.Κ.Δ. ακεραίων αλγεβρικών παραστάσεωνΜέγιστος Κοινός Διαιρέτης ( Μ.Κ.Δ. ) δύο ή περισσοτέρων ακεραίων αλγεβρικών παραστάσεων που έχουν αναλυθεί σε γινόμενο πρώτων παραγόντων ονομάζεται, το γινόμενο των κοινών παραγόντων τους με εκθέτη καθενός το μικρότερο από τους εκθέτες του. Παράδειγμα Μ.Κ.Δ. (6(x2 - y2), 4(x2 - 2χy + y2), 12(x - y)3} = ? Αναλύουμε τις παραστάσεις και τους συντελεστές τους σε γινόμενα πρώτων παραγόντων: $$6\left( {{x^2} - {y^2}} \right) = 2 \cdot 3(x - y)(x + y)$$ $$12{(x - y)^3} = {2^2} \cdot 3{(x - y)^3}$$ $$4({x^2} - 2xy + {y^2}) = {2^2}{(x - y)^2}$$ $${\rm M}.{\rm K}.\Delta .\left( {2 \cdot 3(x - y)(x + y){{,2}^2}{{(x - y)}^2},\,\,{2^2} \cdot 3{{(x - y)}^3}} \right) = 2(x - y)$$
| |
Μεταβλητήλέγεται ένα γράμμα π.χ x,y,z,ω,…( ελληνικό ή λατινικό) που παριστάνει έναν οποιοδήποτε αριθμό. Χρησιμοποιώντας μεταβλητές "μεταφράζουμε" μια φράση σε Αλγεβρική παράσταση. Παράδειγμα: Το άθροισμα δύο αριθμών πολλαπλασιασμένο επί 9. Αν συμβολίσουμε τους αριθμούς x και y τότε το άθροισμά τους είναι x+y και η ζητούμενη αλγεβρική παράσταση 9(x+y).
| |
ΜονώνυμοΜια Ακέραια αλγεβρική παράσταση λέγεται Μονώνυμο, όταν μεταξύ των μεταβλητών της
Για παράδειγμα οι παραστάσεις $$ - 2{x^2}y,\,\,(3 - \sqrt 2 )x{y^3}\,$$ είναι μονώνυμα ενώ οι $$ - 2{x^2}\sqrt y ,\,\,3 - \sqrt 2 x{y^3},\,\,\frac{x}{y}$$ δεν είναι. Ορολογία
.
Πράξεις μονωνύμωνΤο άθροισμα ομοίων μονωνύμων είναι μονώνυμο όμοιο με αυτά και έχει συντελεστή το άθροισμα των συντελεστών τους (Αναγωγή ομοίων όρων). $$2\sqrt 3 {x^2}y - \,\,(2 - \sqrt 3 ){x^2}y - \,\,{x^2}y = $$ Το γινόμενο μονωνύμων είναι μονώνυμο με:
$$2\sqrt 3 {x^2}y\omega \cdot \,( - \frac{1}{6})x{y^2} = $$ Για να διαιρέσουμε μονώνυμα πολλαπλασιάζουμε τον διαιρετέο με τον αντίστροφο του διαιρέτη. $$2\sqrt 3 {x^2}y:\,\left[ {( - \frac{1}{6})x{y^2}\omega } \right] = $$ $$2\sqrt 3 {x^2}y \cdot \,\frac{1}{{( - \frac{1}{6})x{y^2}\omega }} = $$ $$\frac{{2\sqrt 3 }}{{( - \frac{1}{6})}} \cdot \frac{{{x^2}}}{x} \cdot \,\frac{y}{{{y^2}}} \cdot \frac{1}{\omega } = $$ $$ - 12\sqrt {3 \cdot } {x^{2 - 1}} \cdot {y^{1 - 2}} \cdot {\omega ^{ - 1}} = $$ $$\frac{{ - 12\sqrt 3 x}}{{y\omega }}$$ Στη διαίρεση μονωνύμων μπορεί να προκύψει μονώνυμο μικρότερου βαθμού ($$5{x^2}y:\,\,({x^{}}y) = 5x$$), σταθερό μονώνυμο ($$5{x^2}y:\,\,({x^2}y) = 5$$) ή μη ακέραια αλγεβρική παράσταση όπως στο παράδειγμα. | |
Π |
|---|
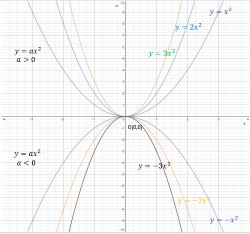
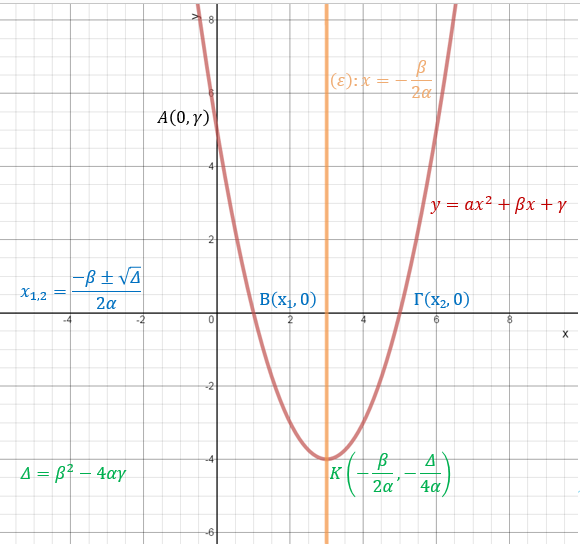
Παραβολή
| |
ΠαραγοντοποίησηΗ διαδικασία με την οποία μια παράσταση, που είναι άθροισμα, μετατρέπεται σε γινόμενο παραγόντων, λέγεται παραγοντοποίηση. Αξιοσημείωτες παραγοντοποιήσειςΠαράσταση δύο όρωνΔιαφορά τετραγώνων: $${\rm{ }}{\alpha ^2} - {\rm{ }}{\beta ^2} = \left( {\alpha {\rm{ + }}\beta } \right)\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)$$$$4{\beta ^2} - 25 = {\left( {2\beta } \right)^{}} - {5^2} = \left( {2\beta + 5} \right)\left( {2\beta - 5} \right)$$ $${\alpha ^6} - {\beta ^6} = {\left( {{\alpha ^3}} \right)^2} - {\left( {{\beta ^3}} \right)^2} = \left( {{\alpha ^3} + {\beta ^3}} \right)\left( {{\alpha ^3} - {\beta ^3}} \right) = \left( {\alpha {\rm{ + }}\beta } \right)\left( {{\alpha ^2}{\rm{ - }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right)\left( {\alpha {\rm{ + }}\beta } \right)\left( {{\alpha ^2}{\rm{ - }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right)$$ $${2014^2} - {1986^2} = (2000 + 14)(2000 - 14) = {2000^2} - {14^2} = 4.000.000 - 196 = 3.999.804$$ Διαφορά κύβων: $${\alpha ^3} - {\rm{ }}{\beta ^3} = \left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)\left( {{\alpha ^2} + {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }}$$$${{\rm{x}}^{\rm{3}}} - 27 = {{\rm{x}}^{\rm{3}}} - {9^3} = \left( {x - 3} \right)\left( {{x^2} - 3x + {3^2}} \right) = \left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right)$$ $${\alpha ^6} - {\beta ^6} = {\left( {{\alpha ^2}} \right)^3} - {\left( {{\beta ^2}} \right)^3} = \left( {{\alpha ^2} - {\beta ^2}} \right)\left[ {{{\left( {{\alpha ^2}} \right)}^2} + {\alpha ^2}{\beta ^2} + {{\left( {{\beta ^2}} \right)}^2}} \right] = \left( {{\alpha ^2} - {\beta ^2}} \right)\left[ {{\alpha ^4} + {\alpha ^2}{\beta ^2} + {\beta ^4}} \right]$$ Άθροισμα κύβων: $${\alpha ^3} - {\rm{ }}{\beta ^3} = \left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)\left( {{\alpha ^2} + {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }}$$$${\alpha ^6} + {\beta ^6} = {\left( {{\alpha ^2}} \right)^3} + {\left( {{\beta ^2}} \right)^3} = \left( {{\alpha ^2} + {\beta ^2}} \right)\left[ {{{\left( {{\alpha ^2}} \right)}^2} - {\alpha ^2}{\beta ^2} + {{\left( {{\beta ^2}} \right)}^2}} \right] = \left( {{\alpha ^2} + {\beta ^2}} \right)\left[ {{\alpha ^4} - {\alpha ^2}{\beta ^2} + {\beta ^4}} \right]$$ Κοινός παράγοντας$${x^5} - x = x\left( {{x^4} - 1} \right) = x\left[ {{{\left( {{x^2}} \right)}^2} - {1^2}} \right] = x\left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right) = x\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)$$ Παράσταση τριών όρωνΤέλειο τετράγωνο αθροίσματος ή διαφοράς: $${\alpha ^2} \pm {\rm{ }}2\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2} = {\left( {\alpha {\rm{ }} \pm {\rm{ }}\beta } \right)^2}$$$${y^4} - {\rm{ }}2{y^2} + {\rm{ }}1 = {\left( {{y^2}} \right)^2} - 2 \cdot \left( {{y^2}} \right) \cdot 1 = {\left( {{y^2} - 1} \right)^2}$$ $$25{\rm{ + }}10{x^3} + {\rm{ }}{x^6} = {5^2} + 2 \cdot 5 \cdot {x^3} + {\left( {{x^3}} \right)^2} = {\left( {5 + {x^3}} \right)^2}$$ Τριώνυμο της μορφής $${x^2} + (\alpha + \beta )x + \alpha \beta $$: $${x^2} + (\alpha + \beta )x + \alpha \beta = (x + \alpha )(x + \beta )$$$${x^2} + {\rm{ }}8x{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}{x^2} + {\rm{ }}\left( {6{\rm{ }} + {\rm{ }}2} \right)x{\rm{ }} + {\rm{ }}6 \cdot 2{\rm{ }} = {\rm{ }}\left( {x{\rm{ }} + {\rm{ }}6} \right)\left( {x{\rm{ }} + {\rm{ }}2} \right)$$ $${x^2} - 5x + 6 = {\rm{ }}{x^2} + \left( { - 3 - 2} \right)x{\rm{ }} + {\rm{ }}( - 3) \cdot ( - 2){\rm{ }} = {\rm{ }}\left( {x - 3} \right)\left( {x - 2{\rm{ }}} \right)$$ Τριώνυμο της μορφής $$\alpha {x^2} + \beta x + \gamma = 0$$ = $$a(x - {\rho _1})(x - {\rho _2})$$ με $${\rho _{1,2}} = \frac{{ - \beta \pm \sqrt {{b^2} - 4a\gamma } }}{{2a}}$$$$2{x^2} + 5x + 3$$. Η εξίσωση $$2{x^2} + 5x + 3 = 0$$ έχει δυο λύσεις, $${\rho _{1,2}} = \frac{{ - 5 \pm \sqrt {{5^2} - 4 \cdot 2 \cdot 3} }}{2}$$, τις $${\rho _1} = - 1$$ και $${\rho _1} = - \frac{3}{2}$$ Έτσι το τριώνυμο γίνεται: $$2{x^2} + 5x + 3 = 2\left[ {x - ( - 1)} \right]\left[ {x - \left( { - \frac{3}{2}} \right)} \right] = 2(x + 1)\left( {x + \frac{3}{2}} \right)$$ Κοινός παράγοντας$$ - 4{y^2} + 4y - 1 = - (4{y^2} - 4y + 1) = - \left[ {{{\left( {2y} \right)}^2} - 2 \cdot \left( {2y} \right) + {1^2}} \right] = - {\left( {2y - 1} \right)^2}$$ $$3{x^3} + 12{x^2} - 15x = 3x({x^2} + 4x - 5) = 3x\left[ {{x^2} + (5 - 1)x + ( - 1) \cdot ( + 5)} \right] = 3x(x + 5)(x - 1)$$ Παράσταση τεσσάρων όρωνΤέλειος κύβος αθροίσματος ή διαφοράς: $${\alpha ^3} \pm 3{\alpha ^2}\beta + 3\alpha {\beta ^2} \pm {\beta ^3} = {(\alpha \pm \beta )^3}$$$$1 - 4y + 8{y^2} - 8{y^3} = {1^3} - 2 \cdot {1^2} \cdot (2y) + 2 \cdot 1 \cdot {(2y)^2} - {(2y)^3} = {(1 - 2y)^3}$$ Ομαδοποίηση 3-1$${x^2} - 2x + 1 - {y^2} = ({x^2} - 2 \cdot x \cdot 1 + {1^2}) - {y^2} = {(x - 1)^2} - {y^2} = (x - 1 - y)(x - 1 + y)$$ Ομαδοποίηση 2-2$$9{x^3} + 9{x^2} - 4x - 4 = 9{x^2}(x + 1) - 4(x + 1) = (x + 1)(9{x^2} - 4) = (x + 1)\left[ {{{(3x)}^2} - {2^2}} \right] = (x + 1)(3x + 2)(3x - 2)$$ Διάσπαση ενός εκ των τριών όρων και δημιουργία τέταρτου$$3{x^2} + 5xy + 2{y^2} = 3{x^2} + 3xy + 2xy + 2{y^2} = 3x(x + y) + 2y(x + y) = (x + y)(3x + 2y)$$ $${\alpha ^4} + {\beta ^4} - 7{\alpha ^2}{\beta ^2} = {\alpha ^4} + {\beta ^4} + 2{\alpha ^2}{\beta ^2} - 9{\alpha ^2}{\beta ^2} = {\left( {{\alpha ^2}} \right)^2} + {\left( {{\beta ^2}} \right)^2} + 2{\alpha ^2}{\beta ^2} - {\left( {3\alpha \beta } \right)^2} = {\left( {{\alpha ^2} + {\beta ^2}} \right)^2} - {\left( {3\alpha \beta } \right)^2} = \left( {{\alpha ^2} + {\beta ^2} - 3\alpha \beta } \right)\left( {{\alpha ^2} + {\beta ^2} + 3\alpha \beta } \right)$$ Παραγοντοποίηση και εξισώσειςΗ παραγοντοποίηση οδηγεί σε παραστάσεις που περιέχουν μόνο γινόμενα $${\rm A} \cdot {\rm B} \cdot \Gamma ...$$. Έτσι η εξίσωση $${\rm A} \cdot {\rm B} \cdot \Gamma ... = 0$$ έχει τις λύσεις: $${\rm A} = 0$$ ή $${\rm B} = 0$$ ή $$\Gamma = 0$$ $$...$$ $${x^2} - 49 = 0 \to {x^2} - {7^2} = 0 \to (x - 7)(x + 7) = 0 \to x - 7 = 0$$ ή $$x + 7 = 0$$ $$ \to $$ $$x = 7$$ ή $$x = - 7$$ | |
Σελίδα: (Προηγούμενο) 1 2 3 (Επόμενο)
ΟΛΑ