Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
Α |
|---|
Ακέραια αλγεβρική παράστασηΜια αλγεβρική παράσταση λέγεται ακέραια, όταν μεταξύ των μεταβλητών της
Για παράδειγμα η παράσταση $$\sqrt 2 {x^2} - \frac{2}{3}x$$ είναι ακέραια ενώ η $$2\sqrt x + 5x$$ δεν είναι. | |
Ακέραιοι αριθμοί
Οι Φυσικοί αριθμοί περιέχονται στους ακεραίους αριθμούς | |
Αλγεβρική παράστασηΜια παράσταση που περιέχει πράξεις με αριθμούς και μεταβλητές ονομάζεται αλγεβρική παράσταση. Όταν γράφουμε αλγεβρικές παραστάσεις, συνήθως δε βάζουμε το σύμβολο (·) του πολλαπλασιασμού μεταξύ των αριθμών και των μεταβλητών ή μεταξύ των μεταβλητών. Έτσι η προηγούμενη παράσταση γράφεται 2x- 5x+5. Oι προσθετέοι 2x & 5x & 5 λέγονται όροι αυτής. Απλοποιούμε τη μορφή των παραστάσεων κάνοντας Αναγωγή ομοίων όρων . | |
Αναγωγή ομοίων όρωνΗ διαδικασία αυτή με την οποία γράφουμε σε απλούστερη μορφή αλγεβρικές παραστάσεις, ονομάζεται «αναγωγή ομοίων όρων». Βασίζεται στην Eπιμεριστική ιδιότητα. 7 · α + 8 · α = (7 + 8) · α = 15 · α | |
ΑνισότηταΣύγκρισηΓια να συγκρίνουμε λοιπόν δύο πραγματικούς αριθμούς α και β, που δεν έχουν παρασταθεί με σημεία ενός άξονα, βρίσκουμε τη διαφορά τους α - β και εξετάζουμε αν είναι θετική ή αρνητική ή μηδέν. Αν α - β > 0 τότε α > β Διάταξη
Δύο ή περισσότεροι πραγματικοί αριθμοί που έχουν παρασταθεί με σημεία ενός άξονα είναι διατεταγμένοι. Άρα: Κάθε θετικός αριθμός είναι μεγαλύτερος από το μηδέν. Ιδιότητες ανισότητας- διάταξης
Αν α > β και γ > 0 τότε α γ > β γ και $$ \frac{ \alpha }{ \gamma } > \frac{ \beta }{ \gamma } $$. Αν πολλαπλασιάσουμε ή διαιρέσουμε και τα δύο μέλη μιας ανισότητας με τον ίδιο θετικό αριθμό, τότε προκύπτει ανισότητα με την ίδια φορά. Αν α > β και γ < 0 τότε α γ < β γ και $$ \frac{ \alpha }{ \gamma } < \frac{ \beta }{ \gamma } $$. Αν πολλαπλασιάσουμε ή διαιρέσουμε και τα δύο μέλη μιας ανισότητας με τον ίδιο αρνητικό αριθμό, τότε προκύπτει ανισότητα αντίθετης φοράς Αν α > β και γ > δ τότε α + γ > β + δ. Αν προσθέσουμε κατά μέλη δύο ή περισσότερες ανισότητες που έχουν την ίδια φορά, τότε προκύπτει ανισότητα με την ίδια φορά.. Αν α, β, γ, δ θετικοί αριθμοί με α > β και γ > δ τότε αγ > βδ. Αν πολλαπλασιάσουμε κατά μέλη δύο ή περισσότερες ανισότητες που έχουν την ίδια φορά και θετικά μέλη, τότε προκύπτει ανισότητα με την ίδια φορά. α2 ≥ 0. Το τετράγωνο κάθε πραγματικού αριθμού α είναι μη αρνητικός αριθμός. Αν για τους πραγματικούς αριθμούς α, β ισχύει α2 + β2 = 0, τότε α = 0 και β = 0. Αν α > β και β > γ τότε α > γ. Μεταβατική ιδιότητα. Δείτε παράδειγμα ασκήσεων με ανισώσεις ... εδώ.
| |
Αριθμητική παράστασηονομάζεται μια παράσταση που περιέχει πράξεις με αριθμούς.. | |
Αρνητικοί αριθμοίΟι αρνητικοί αριθμοί με πρόσημο - , είναι οι συμμετρικοί των θετικών αριθμών, με πρόσημο + (το οποίο παραλείπεται όταν δε δημιουργείται ασάφεια.
Παράσταση των ρητών αριθμών με σημεία μιας ευθείαςΑν θεωρήσουμε αριστερά της αρχής Ο του ημιάξονα Οx των αριθμών, τον αντικείμενο αυτού ημιάξονα Οx', θα έχουμε τη δυνατότητα, με αυτόν τον τρόπο, να παραστήσουμε όλους τους ρητούς αριθμούς. Το σημείο Α έχει τετμημένη 4 και το σημείο Β έχει τετμημένη -2. Πράξεις με αρνητικούς αριθμούςΠρόσθεση
Αφαίρεση
Πολλαπλασιασμός
Διαίρεση
| |
Ά |
|---|
Άρρητοι αριθμοί
| |
Δ |
|---|
ΔιάνυσμαΟρισμοί
Διανύσματα που έχουν την ίδια διεύθυνση. Ομόρροπα - Αντίρροπα, Ίσα - Αντίθετα
Δύο διανύσματα λέγονται ίσα, όταν έχουν την ίδια διεύθυνση, την ίδια φορά και ίσα μέτρα.
Αντίρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και αντίθετη φορά (αντίθετη κατεύθυνση) Δύο διανύσματα είναι αντίθετα, όταν έχουν την ίδια διεύθυνση, ίσα μέτρα και αντίθετη φορά. ΠΡΟΣΟΧΗ: (Τα διανύσματα $$\overrightarrow {{\rm A}{\rm B}} $$ και $$\overrightarrow {{\rm B}{\rm A}} $$ είναι αντίθετα $$\overrightarrow {{\rm A}{\rm B}} = - \overrightarrow {{\rm B}{\rm A}} $$. Έχουν την ίδια διεύθυνση, αντίθετες φορές και ίσα μέτρα $$\left| {\overrightarrow {{\rm A}{\rm B}} } \right| = \left| {\overrightarrow {{\rm B}{\rm A}} } \right|$$). Πρόσθεση διανυσμάτωνΚανόνας παραλληλογράμμου
Κανόνας πολυγώνου
Στο σχήμα ισχύει ότι $$\overrightarrow \alpha + \overrightarrow \beta + \overrightarrow \gamma = \overrightarrow \delta $$.
Αφαίρεση διανυσμάτων
Μηδενικό διάνυσμαΤο μηδενικό διάνυσμα είναι ένα διάνυσμα του οποίου η αρχή και το τέλος (πέρας) ταυτίζονται. Το μηδενικό διάνυσμα συμβολίζεται με $$\overrightarrow 0 $$. Κάθετα διανύσματα. Σύνθεση - Ανάλυση Ουσιαστικά αντικαθιστούμε τα δυο διανύσματα $$\overrightarrow \alpha $$, $$\overrightarrow \beta $$ με ένα $$\overrightarrow \gamma $$ ώστε $$\overrightarrow \alpha + \overrightarrow \beta = \overrightarrow \gamma $$.
Ανάλυση διανύσματος σε δυο συνιστώσες. Αντικαθιστούμε ένα διάνυσμα $$\overrightarrow \gamma $$ με δυο κάθετες συνιστώσες $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$, που έχουν το αρχικό διάνυσμα ως άθροισμα. Χρησιμοποιούνται οι Τριγωνομετρικοί αριθμοί και προκύπτει ότι:
| |

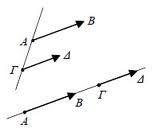 Ομόρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και την ίδια φορά (ἰδια κατεύθυνση)
Ομόρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και την ίδια φορά (ἰδια κατεύθυνση)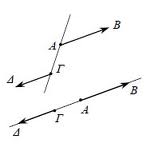
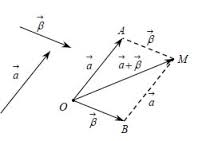 Μεταφέρουμε τα διανύσματα, έτσι ώστε να έχουν κοινή αρχή και σχηματίζουμε το παραλληλόγραμμο που έχει πλευρές τα διανύσματα. Η διαγώνιος του παραλληλογράμμου που έχει ως αρχή την κοινή τους αρχή είναι το άθροισμα των διανυσμάτων.
Μεταφέρουμε τα διανύσματα, έτσι ώστε να έχουν κοινή αρχή και σχηματίζουμε το παραλληλόγραμμο που έχει πλευρές τα διανύσματα. Η διαγώνιος του παραλληλογράμμου που έχει ως αρχή την κοινή τους αρχή είναι το άθροισμα των διανυσμάτων. 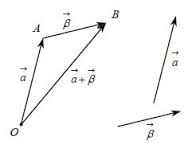
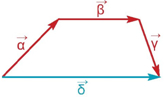 Μεταφέρουμε παράλληλα τα διανύσματα που θέλουμε να προσθέσουμε, ώστε να γίνουν όλα διαδοχικά. Το άθροισμα των θα είναι το
Μεταφέρουμε παράλληλα τα διανύσματα που θέλουμε να προσθέσουμε, ώστε να γίνουν όλα διαδοχικά. Το άθροισμα των θα είναι το 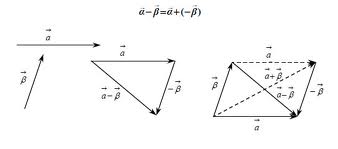 Η διαφορά δύο διανυσμάτων $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$ συμβολίζεται με $$\overrightarrow \alpha - \overrightarrow \beta $$ και ορίζεται ως άθροισμα του $$\overrightarrow \alpha $$ με το αντίθετο
Η διαφορά δύο διανυσμάτων $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$ συμβολίζεται με $$\overrightarrow \alpha - \overrightarrow \beta $$ και ορίζεται ως άθροισμα του $$\overrightarrow \alpha $$ με το αντίθετο