Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ
Π |
|---|
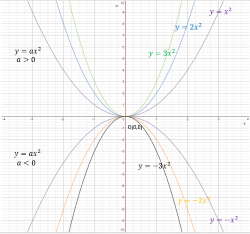
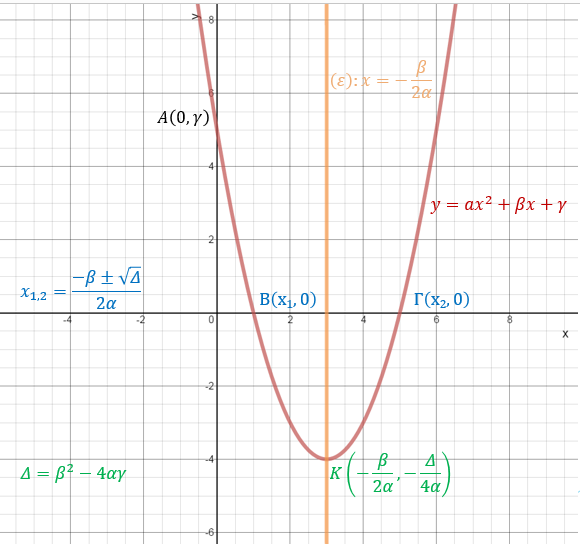
Παραβολή
| |
ΠαραγοντοποίησηΗ διαδικασία με την οποία μια παράσταση, που είναι άθροισμα, μετατρέπεται σε γινόμενο παραγόντων, λέγεται παραγοντοποίηση. Αξιοσημείωτες παραγοντοποιήσειςΠαράσταση δύο όρωνΔιαφορά τετραγώνων: $${\rm{ }}{\alpha ^2} - {\rm{ }}{\beta ^2} = \left( {\alpha {\rm{ + }}\beta } \right)\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)$$$$4{\beta ^2} - 25 = {\left( {2\beta } \right)^{}} - {5^2} = \left( {2\beta + 5} \right)\left( {2\beta - 5} \right)$$ $${\alpha ^6} - {\beta ^6} = {\left( {{\alpha ^3}} \right)^2} - {\left( {{\beta ^3}} \right)^2} = \left( {{\alpha ^3} + {\beta ^3}} \right)\left( {{\alpha ^3} - {\beta ^3}} \right) = \left( {\alpha {\rm{ + }}\beta } \right)\left( {{\alpha ^2}{\rm{ - }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right)\left( {\alpha {\rm{ + }}\beta } \right)\left( {{\alpha ^2}{\rm{ - }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right)$$ $${2014^2} - {1986^2} = (2000 + 14)(2000 - 14) = {2000^2} - {14^2} = 4.000.000 - 196 = 3.999.804$$ Διαφορά κύβων: $${\alpha ^3} - {\rm{ }}{\beta ^3} = \left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)\left( {{\alpha ^2} + {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }}$$$${{\rm{x}}^{\rm{3}}} - 27 = {{\rm{x}}^{\rm{3}}} - {9^3} = \left( {x - 3} \right)\left( {{x^2} - 3x + {3^2}} \right) = \left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right)$$ $${\alpha ^6} - {\beta ^6} = {\left( {{\alpha ^2}} \right)^3} - {\left( {{\beta ^2}} \right)^3} = \left( {{\alpha ^2} - {\beta ^2}} \right)\left[ {{{\left( {{\alpha ^2}} \right)}^2} + {\alpha ^2}{\beta ^2} + {{\left( {{\beta ^2}} \right)}^2}} \right] = \left( {{\alpha ^2} - {\beta ^2}} \right)\left[ {{\alpha ^4} + {\alpha ^2}{\beta ^2} + {\beta ^4}} \right]$$ Άθροισμα κύβων: $${\alpha ^3} - {\rm{ }}{\beta ^3} = \left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)\left( {{\alpha ^2} + {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }}$$$${\alpha ^6} + {\beta ^6} = {\left( {{\alpha ^2}} \right)^3} + {\left( {{\beta ^2}} \right)^3} = \left( {{\alpha ^2} + {\beta ^2}} \right)\left[ {{{\left( {{\alpha ^2}} \right)}^2} - {\alpha ^2}{\beta ^2} + {{\left( {{\beta ^2}} \right)}^2}} \right] = \left( {{\alpha ^2} + {\beta ^2}} \right)\left[ {{\alpha ^4} - {\alpha ^2}{\beta ^2} + {\beta ^4}} \right]$$ Κοινός παράγοντας$${x^5} - x = x\left( {{x^4} - 1} \right) = x\left[ {{{\left( {{x^2}} \right)}^2} - {1^2}} \right] = x\left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right) = x\left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)$$ Παράσταση τριών όρωνΤέλειο τετράγωνο αθροίσματος ή διαφοράς: $${\alpha ^2} \pm {\rm{ }}2\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2} = {\left( {\alpha {\rm{ }} \pm {\rm{ }}\beta } \right)^2}$$$${y^4} - {\rm{ }}2{y^2} + {\rm{ }}1 = {\left( {{y^2}} \right)^2} - 2 \cdot \left( {{y^2}} \right) \cdot 1 = {\left( {{y^2} - 1} \right)^2}$$ $$25{\rm{ + }}10{x^3} + {\rm{ }}{x^6} = {5^2} + 2 \cdot 5 \cdot {x^3} + {\left( {{x^3}} \right)^2} = {\left( {5 + {x^3}} \right)^2}$$ Τριώνυμο της μορφής $${x^2} + (\alpha + \beta )x + \alpha \beta $$: $${x^2} + (\alpha + \beta )x + \alpha \beta = (x + \alpha )(x + \beta )$$$${x^2} + {\rm{ }}8x{\rm{ }} + {\rm{ }}12{\rm{ }} = {\rm{ }}{x^2} + {\rm{ }}\left( {6{\rm{ }} + {\rm{ }}2} \right)x{\rm{ }} + {\rm{ }}6 \cdot 2{\rm{ }} = {\rm{ }}\left( {x{\rm{ }} + {\rm{ }}6} \right)\left( {x{\rm{ }} + {\rm{ }}2} \right)$$ $${x^2} - 5x + 6 = {\rm{ }}{x^2} + \left( { - 3 - 2} \right)x{\rm{ }} + {\rm{ }}( - 3) \cdot ( - 2){\rm{ }} = {\rm{ }}\left( {x - 3} \right)\left( {x - 2{\rm{ }}} \right)$$ Τριώνυμο της μορφής $$\alpha {x^2} + \beta x + \gamma = 0$$ = $$a(x - {\rho _1})(x - {\rho _2})$$ με $${\rho _{1,2}} = \frac{{ - \beta \pm \sqrt {{b^2} - 4a\gamma } }}{{2a}}$$$$2{x^2} + 5x + 3$$. Η εξίσωση $$2{x^2} + 5x + 3 = 0$$ έχει δυο λύσεις, $${\rho _{1,2}} = \frac{{ - 5 \pm \sqrt {{5^2} - 4 \cdot 2 \cdot 3} }}{2}$$, τις $${\rho _1} = - 1$$ και $${\rho _1} = - \frac{3}{2}$$ Έτσι το τριώνυμο γίνεται: $$2{x^2} + 5x + 3 = 2\left[ {x - ( - 1)} \right]\left[ {x - \left( { - \frac{3}{2}} \right)} \right] = 2(x + 1)\left( {x + \frac{3}{2}} \right)$$ Κοινός παράγοντας$$ - 4{y^2} + 4y - 1 = - (4{y^2} - 4y + 1) = - \left[ {{{\left( {2y} \right)}^2} - 2 \cdot \left( {2y} \right) + {1^2}} \right] = - {\left( {2y - 1} \right)^2}$$ $$3{x^3} + 12{x^2} - 15x = 3x({x^2} + 4x - 5) = 3x\left[ {{x^2} + (5 - 1)x + ( - 1) \cdot ( + 5)} \right] = 3x(x + 5)(x - 1)$$ Παράσταση τεσσάρων όρωνΤέλειος κύβος αθροίσματος ή διαφοράς: $${\alpha ^3} \pm 3{\alpha ^2}\beta + 3\alpha {\beta ^2} \pm {\beta ^3} = {(\alpha \pm \beta )^3}$$$$1 - 4y + 8{y^2} - 8{y^3} = {1^3} - 2 \cdot {1^2} \cdot (2y) + 2 \cdot 1 \cdot {(2y)^2} - {(2y)^3} = {(1 - 2y)^3}$$ Ομαδοποίηση 3-1$${x^2} - 2x + 1 - {y^2} = ({x^2} - 2 \cdot x \cdot 1 + {1^2}) - {y^2} = {(x - 1)^2} - {y^2} = (x - 1 - y)(x - 1 + y)$$ Ομαδοποίηση 2-2$$9{x^3} + 9{x^2} - 4x - 4 = 9{x^2}(x + 1) - 4(x + 1) = (x + 1)(9{x^2} - 4) = (x + 1)\left[ {{{(3x)}^2} - {2^2}} \right] = (x + 1)(3x + 2)(3x - 2)$$ Διάσπαση ενός εκ των τριών όρων και δημιουργία τέταρτου$$3{x^2} + 5xy + 2{y^2} = 3{x^2} + 3xy + 2xy + 2{y^2} = 3x(x + y) + 2y(x + y) = (x + y)(3x + 2y)$$ $${\alpha ^4} + {\beta ^4} - 7{\alpha ^2}{\beta ^2} = {\alpha ^4} + {\beta ^4} + 2{\alpha ^2}{\beta ^2} - 9{\alpha ^2}{\beta ^2} = {\left( {{\alpha ^2}} \right)^2} + {\left( {{\beta ^2}} \right)^2} + 2{\alpha ^2}{\beta ^2} - {\left( {3\alpha \beta } \right)^2} = {\left( {{\alpha ^2} + {\beta ^2}} \right)^2} - {\left( {3\alpha \beta } \right)^2} = \left( {{\alpha ^2} + {\beta ^2} - 3\alpha \beta } \right)\left( {{\alpha ^2} + {\beta ^2} + 3\alpha \beta } \right)$$ Παραγοντοποίηση και εξισώσειςΗ παραγοντοποίηση οδηγεί σε παραστάσεις που περιέχουν μόνο γινόμενα $${\rm A} \cdot {\rm B} \cdot \Gamma ...$$. Έτσι η εξίσωση $${\rm A} \cdot {\rm B} \cdot \Gamma ... = 0$$ έχει τις λύσεις: $${\rm A} = 0$$ ή $${\rm B} = 0$$ ή $$\Gamma = 0$$ $$...$$ $${x^2} - 49 = 0 \to {x^2} - {7^2} = 0 \to (x - 7)(x + 7) = 0 \to x - 7 = 0$$ ή $$x + 7 = 0$$ $$ \to $$ $$x = 7$$ ή $$x = - 7$$ | |
ΠολυώνυμοΜια αλγεβρική παράσταση λέγεται Πολυώνυμο, όταν μεταξύ των μεταβλητών της
Για παράδειγμα η παράσταση $$2{x^2}y + 3{x^2}y - x{y^2} - 2x{y^2}$$ είναι το πολυώνυμο $$5{x^2}y - 3x{y^2}$$. Ορολογία
.
Πράξεις πολυωνύμωνΜπορούμε να προσθέσουμε, να αφαιρέσουμε, ή να πολλαπλασιάσουμε πολυώνυμα, χρησιμοποιώντας τις ιδιότητες των πραγματικών αριθμών, όπως φαίνεται στα επόμενα παραδείγματα: Πρόσθεση (x3 + 2x2 - 5x + 7) + (4x3 - 5x2 + 3) = = x3 + 2x2 - 5x + 7 + 4x3 - 5x2 + 3 = = (1 + 4)x3 + (2 - 5)x2 - 5x + (7 + 3) = = 5x3 - 3x2 - 5x + 10 [Πολυώνυμο 3ου βαθμού]
(2x3 - x2 + 1) + (-2x3 + 2x - 3) = = 2x3 - x2 + 1 - 2x3 + 2x - 3 = = -x2 + 2x - 2 [Πολυώνυμο 2ου βαθμού]
(x3 - 3x2 - 1) + (-x3 + 3x2 + 1) = = x3 - 3x2 - 1 - x3 + 3x2 + 1 = 0 [Μηδενικό πολυώνυμο]
Αφαίρεση (x3 + 2x2 - 5x + 7) - (4x3 - 5x2 + 3) = x3 + 2 x2 - 5x + 7 - 4x3 + 5x2 - 3 = -3x3 + 7x2 - 5x + 4 [Πολυώνυμο 3ου βαθμού]
Πολλαλασιασμός
(x2 + 5x)(2x3 + 3x - 1) =
= x2(2x3 + 3x - 1) + 5x(2x3 + 3x - 1) = 2x5 + 3x3 - x2 + 10x4 + 15x2 - 5x = 2x5 + 10x4 + 3x3 + 14x2 - 5x [Πολυώνυμο 5ου βαθμού] Για το βαθμό του αθροίσματος και του γινομένου δυο πολυωνύμων ισχύει ότι:
Διαίρεση
Δείτε παραδείγματα διαίρεσης
| |
Πραγματικοί αριθμοίΟι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς Άξονας πραγματικών αριθμών
Οι ακέραιοι αριθμοί: ... -3, -2, -1, 0, 1, 2, 3 ... παριστάνονται πάλι με σημεία. Το σύνολο των ρητών αριθμών, δηλαδή των αριθμών που μπορούν να γραφούν στη μορφή, όπου μ ακέραιος και ν φυσικός αριθμός. Οι ρητοί αριθμοί έχουν γνωστή δεκαδική μορφή και γεμίζουν την ευθεία, αλλά όχι πλήρως. Οι πραγματικοί αριθμοί αποτελούνται όχι μόνο από τους ρητούς αλλά και όλους τους άρρητους.
| |
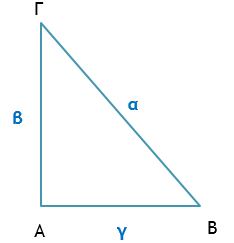 Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.
Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.