Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ
Σελίδα: (Προηγούμενο) 1 2 3
ΟΛΑ
Π |
|---|
ΠολυώνυμοΜια αλγεβρική παράσταση λέγεται Πολυώνυμο, όταν μεταξύ των μεταβλητών της
Για παράδειγμα η παράσταση $$2{x^2}y + 3{x^2}y - x{y^2} - 2x{y^2}$$ είναι το πολυώνυμο $$5{x^2}y - 3x{y^2}$$. Ορολογία
.
Πράξεις πολυωνύμωνΜπορούμε να προσθέσουμε, να αφαιρέσουμε, ή να πολλαπλασιάσουμε πολυώνυμα, χρησιμοποιώντας τις ιδιότητες των πραγματικών αριθμών, όπως φαίνεται στα επόμενα παραδείγματα: Πρόσθεση (x3 + 2x2 - 5x + 7) + (4x3 - 5x2 + 3) = = x3 + 2x2 - 5x + 7 + 4x3 - 5x2 + 3 = = (1 + 4)x3 + (2 - 5)x2 - 5x + (7 + 3) = = 5x3 - 3x2 - 5x + 10 [Πολυώνυμο 3ου βαθμού]
(2x3 - x2 + 1) + (-2x3 + 2x - 3) = = 2x3 - x2 + 1 - 2x3 + 2x - 3 = = -x2 + 2x - 2 [Πολυώνυμο 2ου βαθμού]
(x3 - 3x2 - 1) + (-x3 + 3x2 + 1) = = x3 - 3x2 - 1 - x3 + 3x2 + 1 = 0 [Μηδενικό πολυώνυμο]
Αφαίρεση (x3 + 2x2 - 5x + 7) - (4x3 - 5x2 + 3) = x3 + 2 x2 - 5x + 7 - 4x3 + 5x2 - 3 = -3x3 + 7x2 - 5x + 4 [Πολυώνυμο 3ου βαθμού]
Πολλαλασιασμός
(x2 + 5x)(2x3 + 3x - 1) =
= x2(2x3 + 3x - 1) + 5x(2x3 + 3x - 1) = 2x5 + 3x3 - x2 + 10x4 + 15x2 - 5x = 2x5 + 10x4 + 3x3 + 14x2 - 5x [Πολυώνυμο 5ου βαθμού] Για το βαθμό του αθροίσματος και του γινομένου δυο πολυωνύμων ισχύει ότι:
Διαίρεση
Δείτε παραδείγματα διαίρεσης
| |
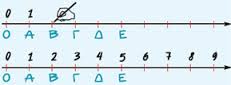
Πραγματικοί αριθμοίΟι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς Άξονας πραγματικών αριθμών
Οι ακέραιοι αριθμοί: ... -3, -2, -1, 0, 1, 2, 3 ... παριστάνονται πάλι με σημεία. Το σύνολο των ρητών αριθμών, δηλαδή των αριθμών που μπορούν να γραφούν στη μορφή, όπου μ ακέραιος και ν φυσικός αριθμός. Οι ρητοί αριθμοί έχουν γνωστή δεκαδική μορφή και γεμίζουν την ευθεία, αλλά όχι πλήρως. Οι πραγματικοί αριθμοί αποτελούνται όχι μόνο από τους ρητούς αλλά και όλους τους άρρητους.
| |
Ρ |
|---|
Ρητή αλγεβρική παράστασηΜια αλγεβρική παράσταση που είναι κλάσμα με όρους πολυώνυμα, λέγεται ρητή αλγεβρικήπαράσταση ή απλώς ρητή παράσταση. π.χ. $$A = \frac{{3{x^2} + 12x + 12}}{{{x^2} - 4}}$$ Οι μεταβλητές μιας ρητής παράστασης δεν μπορούν να πάρουν τιμές που μηδενίζουν τον παρονομαστή. $${x^2} - 4 \ne 0$$ ή $${x^2} \ne 4$$ ή $$x \ne \sqrt 4 $$ ή $$x \ne \pm 2$$. Η μεταβλητή x μπορεί να έχει ως τιμή κάθε πραγματικό αριθμός εκτός των -2, +2. Για να απλοποιήσουμε μια ρητή αλγεβρική παράσταση, παραγοντοποιούμε και τους δύο όρους της και διαγράφουμε τον κοινό παράγοντα. $$A = \frac{{3{x^2} + 12x + 12}}{{{x^2} - 4}} = \frac{{3\left( {{x^2} + 4x + 4} \right)}}{{{x^2} - 4}} = \frac{{3\left( {{x^2} + 2 \cdot 2 \cdot x + {2^2}} \right)}}{{{x^2} - {2^2}}} = \frac{{3{{(x + 2)}^2}}}{{(x - 2)(x + 2)}} = \frac{{3(x + 2)}}{{x - 2}}$$ Οι πράξεις με τις ρητές παραστάσεις γίνονται όπως και οι πράξεις των αριθμητικών κλασμάτων. | |
Ρητοί αριθμοί
Μορφή ρητού αριθμού: $$ \frac{ \mu }{ \nu } $$ με ν ≠ 0 κια Μ.Κ.Δ. (μ,ν) =1 Κάθε ρητός αριθμός μπορεί να γραφεί και σε δεκαδική μορφή. Αυτό γίνεται κάνοντας τη διαίρεση μ / ν. Η διαίρεση αυτή μπορεί
Οι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς
| |
Τ |
|---|
ΤαυτότηταΤαυτότητα λέγεται κάθε ισότητα που περιέχει μεταβλητές και αληθεύει για όλες τις τιμές των μεταβλητών της. Αξιοσημείωτες ταυτότητεςΤο δεύτερα μέλη των ταυτοτήτων που ακολουθούν ονομάζονται αναπτύγματα. Τετράγωνο αθροίσματος$${\left( {\alpha {\rm{ }} + {\rm{ }}\beta } \right)^2} = {\rm{ }}{\alpha ^2} + {\rm{ }}2\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}$$ $${\left( {y{\rm{ }} + {\rm{ }}4} \right)^2} = {\rm{ }}{y^2} + {\rm{ }}2 \cdot y \cdot 4{\rm{ }} + {\rm{ }}{4^2} = {\rm{ }}{y^2} + {\rm{ }}8y{\rm{ }} + {\rm{ }}16$$ $${\left( {\sqrt 3 + 1} \right)^2} = {\left( {\sqrt 3 } \right)^2} + {\rm{ }}2 \cdot \sqrt 3 \cdot 1{\rm{ }} + {\rm{ }}{{\rm{1}}^2} = {\rm{ }}3 + {\rm{ }}2\sqrt 3 {\rm{ }} + {\rm{ }}1 = 4 + 2\sqrt 3 {\rm{ }}$$
Τετράγωνο διαφοράς$${\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)^2} = {\rm{ }}{\alpha ^2} - {\rm{ }}2\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}$$ $${\left( {\omega - \frac{2}{\omega }} \right)^2} = {\omega ^2} - 2 \cdot \omega \cdot \frac{2}{\omega } + {\left( {\frac{2}{\omega }} \right)^2} = {\omega ^2} - 4 + \frac{4}{{{\omega ^2}}}$$ $${\left( {1 - \sqrt 7 } \right)^2} = 1 - 2 \cdot 1 \cdot \sqrt 7 + {\left( {\sqrt 7 } \right)^2} = {\rm{ }}3 - {\rm{ }}2\sqrt 7 {\rm{ }} + {\rm{ 7}} = 10 - 2\sqrt 7 {\rm{ }}$$
Κύβος αθροίσματος$${\left( {\alpha {\rm{ }} + {\rm{ }}\beta } \right)^3} = {\rm{ }}{\alpha ^3} + {\rm{ }}3{\alpha ^2}\beta + 3\alpha {\beta ^2} + {\beta ^3}$$ $${\left( {{\rm{2x }} + {\rm{ 1}}} \right)^3} = {\rm{ }}{\left( {2x} \right)^3} + {\rm{ }}3 \cdot {\left( {2x} \right)^2} \cdot 1 + 3 \cdot \left( {2x} \right) \cdot {1^2} + {1^3} = 8{x^3} + 12{x^2} + 6x + 1$$ $${\left( {\sqrt {\rm{2}} {\rm{ }} + {\rm{ 1}}} \right)^3} = {\rm{ }}{\left( {\sqrt {\rm{2}} } \right)^3} + {\rm{ }}3 \cdot {\left( {\sqrt {\rm{2}} } \right)^2} \cdot 1 + 3 \cdot \left( {\sqrt {\rm{2}} } \right) \cdot {1^2} + {1^3} = {\left( {\sqrt {\rm{2}} } \right)^2} \cdot \sqrt {\rm{2}} + 3 \cdot 2 \cdot 1 + 3\sqrt 2 + 1 = 2\sqrt {\rm{2}} + 6 + 3\sqrt 2 + 1 = 5\sqrt {\rm{2}} + 7$$
Κύβος διαφοράς$${\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)^3} = {\rm{ }}{\alpha ^3} - {\rm{ }}3{\alpha ^2}\beta + 3\alpha {\beta ^2} - {\beta ^3}$$ $${\left( {{\omega ^2} - {\rm{ }}2\omega } \right)^3} = {\left( {{\omega ^2}} \right)^3} - {\rm{ }}3 \cdot {\left( {{\omega ^2}} \right)^2} \cdot \left( {2\omega } \right) + 3 \cdot \left( {{\omega ^2}} \right) \cdot {\left( {2\omega } \right)^2} - {\left( {2\omega } \right)^3} = {\omega ^6} - 3 \cdot \left( {{\omega ^4}} \right) \cdot \left( {2\omega } \right) + 3 \cdot \left( {{\omega ^2}} \right) \cdot \left( {4{\omega ^2}} \right) - 8{\omega ^3} = {\omega ^6} - 6{\omega ^5} + 12{\omega ^4} - 8{\omega ^3}$$ $${\left( {\sqrt {\rm{2}} {\rm{ - }}\sqrt {\rm{3}} } \right)^3} = {\rm{ }}{\left( {\sqrt {\rm{2}} } \right)^3}{\rm{ - }}3 \cdot {\left( {\sqrt {\rm{2}} } \right)^2} \cdot \sqrt {\rm{3}} + 3 \cdot \left( {\sqrt {\rm{2}} } \right) \cdot {\left( {\sqrt {\rm{3}} } \right)^2} - {\left( {\sqrt {\rm{3}} } \right)^3} = {\left( {\sqrt {\rm{2}} } \right)^2} \cdot \sqrt {\rm{2}} - 3 \cdot 2 \cdot \sqrt {\rm{3}} + 3 \cdot \sqrt 2 \cdot 3 - {\left( {\sqrt {\rm{3}} } \right)^2} \cdot \sqrt {\rm{3}} = 2\sqrt {\rm{2}} - 6\sqrt {\rm{3}} + 9\sqrt 2 - 3\sqrt {\rm{3}} = 11\sqrt 2 - 9\sqrt {\rm{3}} $$
Γινόμενο αθροίσματος επί διαφορά$$\left( {\alpha {\rm{ + }}\beta } \right)\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right){\rm{ = }}{\alpha ^2} - {\rm{ }}{\beta ^2}$$ $$\left( {{\alpha ^3}{\rm{ + }}{\beta ^3}} \right)\left( {{\alpha ^3}{\rm{ }} - {\rm{ }}{\beta ^3}} \right){\rm{ = }}{\left( {{\alpha ^3}} \right)^2} - {\rm{ }}{\left( {{\beta ^3}} \right)^2} = {\alpha ^6}{\rm{ }} - {\rm{ }}{\beta ^6}$$ $$99 \cdot 101 = \left( {100 - 1} \right)\left( {100 + 1} \right) = {100^2} - {1^2} = 10000 - 1 = 9999$$
Τα γινόμενα του αθροίσματος ή της διαφοράς κύβων$$\left( {\alpha {\rm{ }} + {\rm{ }}\beta } \right)\left( {{\alpha ^2} - {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }} = {\rm{ }}{\alpha ^3} + {\rm{ }}{\beta ^3}$$ $$\left( {x{\rm{ }} + {\rm{ }}3} \right)\left( {{x^2} - {\rm{ }}3x{\rm{ }} + {\rm{ }}9} \right){\rm{ }} = {\rm{ }}\left( {x{\rm{ }} + {\rm{ }}3} \right)\left( {{x^2} - {\rm{ }}3x{\rm{ }} + {\rm{ }} + {\rm{ }}{3^2}} \right){\rm{ }} = {\rm{ }}{x^3} + {\rm{ }}{3^3} = {\rm{ }}{x^3} + {\rm{ }}27$$ $$\left( {\alpha {\rm{ }} - {\rm{ }}\beta } \right)\left( {{\alpha ^2} + {\rm{ }}\alpha \beta {\rm{ }} + {\rm{ }}{\beta ^2}} \right){\rm{ }} = {\rm{ }}{\alpha ^3} - {\rm{ }}{\beta ^3}$$ $$\left( {x{\rm{ }} - {\rm{ }}2} \right)\left( {{x^2} + {\rm{ }}2x{\rm{ }} + {\rm{ }}4} \right){\rm{ }} = {\rm{ }}\left( {x{\rm{ }} - {\rm{ }}2} \right)\left( {{x^2} + {\rm{ }}2x{\rm{ }} + {\rm{ }} + {\rm{ }}{2^2}} \right){\rm{ }} = {\rm{ }}{x^3} - {\rm{ }}{2^3} = {\rm{ }}{x^3}{\rm{ }} - {\rm{ }}8$$ | |
Τετραγωνική ρίζαΤετρ. ρίζα ενός θετικού αριθμού α, λέγεται ο θετικός αριθμός, ο οποίος, όταν υψωθεί στο τετράγωνο, δίνει τον αριθμό α. Η τετρ. ρίζα του α συμβολίζεται με $$ \sqrt{ \alpha } $$.
Ιδιότητες
Προσοχή!
Χρήσιμες ιδιότητες για την απλοποίηση παραστάσεων Ρίζα δύναμης με άρτιο εκθέτη: $$\sqrt {{\alpha ^{2\nu }}} = \sqrt {{{\left( {{\alpha ^\nu }} \right)}^2}} = {\alpha ^\nu }$$
| |
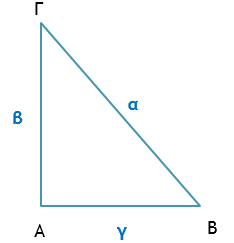
Τριγωνομετρικοί αριθμοίΟρισμοίΓια τις οξείες γωνίες ενός ορθογωνίου τριγώνου δίνονται οι εξής ορισμοί. $${\rm E}\Phi {\rm A}\Pi {\rm T}{\rm O}{\rm M}{\rm E}{\rm N}{\rm H} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}$$ $${\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$ $$\Sigma \Upsilon {\rm N}{\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$
$$\begin{array}{l}\varepsilon \varphi {\rm B} = \frac{{{\rm A}\Gamma }}{{{\rm A}{\rm B}}} = \frac{\beta }{\gamma }\,\,\,\,\,\,\,\,\,\,\,\,\varepsilon \varphi \Gamma = \frac{{{\rm A}{\rm B}}}{{{\rm A}\Gamma }} = \frac{\gamma }{\beta }\\\eta \mu {\rm B} = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\eta \mu \Gamma = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\\\sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\end{array}$$ Γνωρίζουμε ότι σε κάθε ορθογώνιο τρίγωνο η υποτείνουσα είναι μεγαλύτερη από καθεμία από τις κάθετες πλευρές. Επομένως ισχύουν οι ανισώσεις: 0 < ημω < 1 και 0 < συνω < 1
Σχέσεις τριγωνομετρικών αριθμώνΓια κάθε γωνία ισχύει ότι $$\varepsilon \varphi \omega = \frac{{\eta \mu \omega }}{{\sigma \upsilon \nu \omega }}\,\,\,\,\left\{ {\frac{{\eta \mu \Gamma }}{{\sigma \upsilon \nu \Gamma }} = \frac{{\frac{\gamma }{\alpha }}}{{\frac{\beta }{\alpha }}} = \frac{{\gamma \cdot \alpha }}{{\beta \cdot \alpha }} = \frac{\gamma }{\beta } = \varepsilon \varphi \Gamma } \right\}$$ Όπως φαίνεται $$\eta \mu {\rm B} = \sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,$$ και $$\eta \mu \Gamma = \sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }$$, δηλαδή το ημίτονο μιας γωνίας ισούται με το συνημίτονο της συμπληρωματικής της. Παρατηρήστε ότι $$\,\varepsilon \varphi \Gamma = \frac{1}{{\varepsilon \varphi {\rm B}}}$$, δηλαδή οι εφαπτομένες συμπληρωματικών γωνιών είναι αριθμοί αντίστροφοι, έχουν γινόμενο 1 $$\varepsilon \varphi {\rm B} \cdot \varepsilon \varphi \Gamma = \frac{\gamma }{\beta } \cdot \frac{\beta }{\gamma } = 1\,$$. Μεταβολές τριγωνομετρικών αριθμών οξειών γωνιώνΌταν μια οξεία γωνία αυξάνεται↑, τότε: αυξάνεται το ημίτονό↑ της, ελαττώνεται το συνημίτονό↓ της και αυξάνεται η εφαπτομένη↑ της. Χαρακτηριστικές τιμές τριγωνομετρικών αριθμών οξειών γωνιών$$\begin{array}{ccccccccccccccc}{}&{{{30}^o}}&{{{45}^o}}&{{{60}^o}}\\{\eta \mu }&{\frac{1}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 3 }}{2}}\\{\sigma \upsilon \nu }&{\frac{{\sqrt 3 }}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{1}{2}}\\{\varepsilon \varphi }&{\frac{{\sqrt 3 }}{3}}&1&{\sqrt 3 }\end{array}$$ | |
Υ |
|---|
Υπερβολή
Και στις δύο περιπτώσεις η γραφική παράσταση μιας υπερβολής έχει:
Όταν οι μεταβλητές x , y εκφράζουν ποσά / μεγέθη, τότε τα ποσά / μεγέθη αυτά είναι αντιστρόφως ανάλογα, το γινόμενό τους είναι η σταθερά α. Δεἰτε ένα παράδειγμα αντιστρόφως ποσών και τη μελέτη με τη χρήση συναρτήσεων και γραφικών... εδώ. | |
Φ |
|---|
Φυσικοί αριθμοίΟι αριθμοί 0, 1, 2, 3, 4, 5, 6......... 98, 99, 100........ 1999, 2000, 2001, ... ονομάζονται φυσικοί αριθμοί.
Κάθε φυσικός αριθμός έχει έναν επόμενο και ένα προηγούμενο φυσικό αριθμό, εκτός από το 0 που έχει μόνο επόμενο, το 1. Περισσότερα... | |
Σελίδα: (Προηγούμενο) 1 2 3
ΟΛΑ
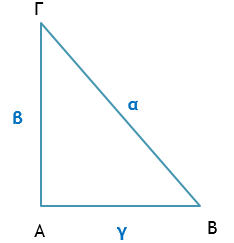 Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.
Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.