Αλγεβρική παράσταση Μια παράσταση που περιέχει πράξεις με αριθμούς και μεταβλητές ονομάζεται αλγεβρική παράσταση.
Για παράδειγμα, η παράσταση 2·x- 5·x+5 είναι μια αλγεβρική παράσταση.
Όταν γράφουμε αλγεβρικές παραστάσεις, συνήθως δε βάζουμε το σύμβολο (·) του πολλαπλασιασμού μεταξύ των αριθμών και των μεταβλητών ή μεταξύ των μεταβλητών. Έτσι η προηγούμενη παράσταση γράφεται 2x- 5x+5.
Oι προσθετέοι 2x & 5x & 5 λέγονται όροι αυτής.
Απλοποιούμε τη μορφή των παραστάσεων κάνοντας Αναγωγή ομοίων όρων . |
|
Αναγωγή ομοίων όρων Η διαδικασία αυτή με την οποία γράφουμε σε απλούστερη μορφή αλγεβρικές παραστάσεις, ονομάζεται «αναγωγή ομοίων όρων». Βασίζεται στην Eπιμεριστική ιδιότητα.
7 · α + 8 · α = (7 + 8) · α = 15 · α
x + 4 · x – 2 · x = (1 + 4 – 2) · x = 3 · x
5 · t – 6 · t – 8 · t = (5 – 6 – 8) · t = –9 · t |
|
Μεταβλητή λέγεται ένα γράμμα π.χ x,y,z,ω,…( ελληνικό ή λατινικό) που παριστάνει έναν οποιοδήποτε αριθμό.
Χρησιμοποιώντας μεταβλητές "μεταφράζουμε" μια φράση σε Αλγεβρική παράσταση.
Παράδειγμα: Το άθροισμα δύο αριθμών πολλαπλασιασμένο επί 9. Αν συμβολίσουμε τους αριθμούς x και y τότε το άθροισμά τους είναι x+y και η ζητούμενη αλγεβρική παράσταση 9(x+y).
|
|
Ακέραιοι αριθμοί  Ακέραιοι αριθμοί είναι οι φυσικοί αριθμοί μαζί με τους αντίστοιχους αρνητικούς αριθμούς. Ακέραιοι αριθμοί είναι οι φυσικοί αριθμοί μαζί με τους αντίστοιχους αρνητικούς αριθμούς.
Οι Φυσικοί αριθμοί περιέχονται στους ακεραίους αριθμούς |
|
Ανίσωση Ονομάζουμε ανίσωση την ανισότητα δύο αλγεβρικών παραστάσεων που περιέχουν τουλάχιστον μια μεταβλητή που ονομάζεται άγνωστος.
π.χ. ανίσωση είναι η παράσταση 2x+5x-3≥8(x+2)
- Η αλγεβρική παράσταση αριστερά ή δεξιά του ίσον λέγεται μέλος της ανίσωσης.
- Οι όροι που περιέχουν μεταβλητή λέγονται άγνωστοι όροι (2x, 5x, x), ενώ οι άλλοι λέγονται γνωστοί όροι.
- Λύση ή ρίζα της ανίσωσης είναι η τιμές του αγνώστου που επαληθεύουν την ανιισότητα.
- Η διαδικασία αναζήτησης της λύσης της ανίσωσης λέγεται επίλυση της ανίσωσης.
Δείτε παράδειγμα ασκήσεων με ανισώσεις ... εδώ. |
|
Απόλυτη τιμή 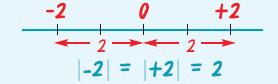 Η απόλυτη τιμή ενός ρητού αριθμού α εκφράζει την απόσταση του σημείου μετετμημένη α από την αρχή Ο του άξονα και συμβολίζεται με |α|. Η απόλυτη τιμή ενός ρητού αριθμού α εκφράζει την απόσταση του σημείου μετετμημένη α από την αρχή Ο του άξονα και συμβολίζεται με |α|.
Αντίθετοι ονομάζονται δύο αριθμοί που είναι ετερόσημοι και έχουν την ίδια απόλυτη τιμή.
Ο αντίθετος του x είναι ο -x.
H απόλυτη τιμή ενός θετικού αριθμού είναι ο ίδιος ο αριθμός. |+6| = 6.
H απόλυτη τιμή ενός αρνητικού αριθμού είναι ο αντίθετός του. |-6| = -(6-)=6
H απόλυτη τιμή του μηδενός είναι το μηδέν. |
|
Αριθμητική παράσταση ονομάζεται μια παράσταση που περιέχει πράξεις με αριθμούς..
Για παράδειγμα, η παράσταση 2·3-4·(-3)+5 είναι μια αριθμητική παράσταση. |
|
Αρνητικοί αριθμοί Οι αρνητικοί αριθμοί με πρόσημο - , είναι οι συμμετρικοί των θετικών αριθμών, με πρόσημο + (το οποίο παραλείπεται όταν δε δημιουργείται ασάφεια.
- Το μηδέν δεν είναι ούτε θετικός ούτε αρνητικός αριθμός
- Ομόσημοι λέγονται οι αριθμοί που έχουν το ίδιο πρόσημο. +5 , +1,25 , +$$ \frac{5}{7} $$ ή -5 , -1,25 , -$$ \frac{5}{7} $$
- Ετερόσημοι λέγονται οι αριθμοί που έχουν διαφορετικό πρόσημο. -5 , +7,2
Παράσταση των ρητών αριθμών με σημεία μιας ευθείας
Αν θεωρήσουμε αριστερά της αρχής Ο του ημιάξονα Οx των αριθμών, τον αντικείμενο αυτού ημιάξονα Οx', θα έχουμε τη δυνατότητα, με αυτόν τον τρόπο, να παραστήσουμε όλους τους ρητούς αριθμούς.

Το σημείο Α έχει τετμημένη 4 και το σημείο Β έχει τετμημένη -2.
Απόλυτη τιμή
Πράξεις με αρνητικούς αριθμούς
Πρόσθεση
- Αν οι αριθμοί είναι ομόσημοι, προσθέτουμε τις απόλυτες τιμές τους και στο άθροισμα βάζουμε το κοινό τους πρόσημο: +2+3=+(2+3)=+5 , -2-3=-(2+3)=-5
- Αν οι αριθμοί είναι ετερόσημοι, αφαιρούμε τη μικρότερη απόλυτη τιμή από τη μεγαλύτερη και στη διαφορά βάζουμε το πρόσημο της μεγαλύτερη απόλυτης τιμής: -2+3=+(3-2) =+1 , +2-3=-(3-2)=-1
Αφαίρεση
- Στον μειωτέο α, πρσθέτουμα τον αντίθετο του αφαιρετέου. α-β=α+(-β): 2-(-3)=2+(+3)=+5 , 2-(+3)=2+(-3)=-1
Πολλαπλασιασμός
- Αν οι αριθμοί είναι ομόσημοι, πολλαπλασιάζουμε τις απόλυτες τιμές τους και στο γινόμενο βάζουμε θετικό πρόσημο: (+2)·(+3)=+6 , (-2)·(-3)=+6
- Αν οι αριθμοί είναι ετερόσημοι, πολλαπλασιάζουμε τις απόλυτες τιμές τους και στο γινόμενο βάζουμε αρνητικό πρόσημο: (+2)·(-3)=-6 , (-2)·(+3)=-6
Διαίρεση
- Πολλαπλασιάζουμε τον διαιρετέο α με τον αντίστροφο $$ \frac{1}{ \beta } $$ του διαιρέτη β. α:β= $$ \alpha \cdot \frac{1}{ \beta } $$, με β≠0.
- Για τα πρόσημα ισχύει ο κανόνας του πολλαπλασιασμού.
- (+3): (-$$ \frac{3}{5} $$) = (+3)·(-$$ \frac{5}{3} $$) =-5
|
|
Άρρητοι αριθμοί 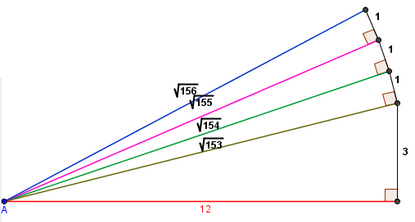 Κάθε αριθμός που δεν είναι ρητός, ονομάζεται άρρητος αριθμός. Κάθε αριθμός που δεν είναι ρητός, ονομάζεται άρρητος αριθμός.
- Οι άρρητοι αριθμοί δεν μπορούν να γραφούν στη μοεφή $$ \frac{ \mu }{ \nu } $$ με ν ≠ 0.
- Η δεκαδική φραφή του άρρητου αριθμού έχει άπειρα ψηφία, χωρίς να εμφανίζεται επαναλαμβανόμενο μοτίβο.
- η τετραγωνική ρίζα κάθε ακέραιου που δεν είναι τετράγωνο, είναι άρρητος.
- Υπάρχουν και άλλοι άρρητοι που δεν είναι ρίζες ρητών αριθμών, όπως ο γνωστός από τη μέτρηση του κύκλου αριθμός π.
|
|
Δύναμη Δυνάμεις ρητών αριθμών με φυσικό εκθέτη

- Για ν = 1, γράφουμε α0 = 1
- Για ν = 1, γράφουμε α1 = α
- Η δύναμη αν διαβάζεται και νιοστή δύναμη του α.
- Η δύναμη α2 λέγεται και τετράγωνο του α ή α στο τετράγωνο.
- Η δύναμη α3 λέγεται κύβος του α ή α στον κύβο.
Πρόσημο δύναμης
- Δύναμη με βάση θετικό αριθμό είναι θετικός αριθμός. Αν α > 0, τότε αν > 0, (+2)3 = +23
- Δύναμη με βάση αρνητικό αριθμό και εκθέτη άρτιο είναι θετικός αριθμός. Αν α < 0 και ν άρτιος, τότε αν> 0, (-2)4 = +24
- Δύναμη με βάση αρνητικό αριθμό και εκθέτη περιττό είναι αρνητικός αριθμός. Αν α < 0 και ν περιττός, τότε αν< 0, (-2)3 = -23
Δυνάμεις ρητών αριθμών με ακέραιο εκθέτη
- Η δύναμη κάθε αριθμού, διάφορου του μηδενός, με εκθέτη αρνητικό είναι ίση με δύναμη μου έχει βάση τον αντίστροφο αριθμό με αντίθετο εκθέτη.
$$\left( \frac{ \alpha }{ \beta } \right)^{-\ ν}$$=$$\left( \frac{ \beta }{ \alpha } \right)^{\ ν}$$ , $$\left( \frac{ 2 }{ 3 } \right)^{-\ 5}$$=$$\left( \frac{ 3 }{ 2 } \right)^{\ 5}$$
Ιδιότητες δυνάμεων
- Για να πολλαπλασιάσουμε δυνάμεις με την ίδια βάση, αφήνουμε την ίδια βάση και βάζουμε εκθέτη το άθροισμα των εκθετών. αμ · αν = αμ+ν
32 · 33 = 35, 32 · 3- 3 = 3- 1 = $$ \frac{1}{3} $$
- Για να διαιρέσουμε δυνάμεις με την ίδια βάση, αφήνουμε την ίδια βάση και βάζουμε εκθέτη τη διαφορά του εκθέτη του διαιρέτη από τον εκθέτη του διαιρετέου. αμ : αν = αμ - ν
32 : 33 = 3-1 = $$ \frac{1}{3} $$, 32 : 3- 3 = 32 - (-3) = 35
- Για να υψώσουμε ένα γινόμενο σε εκθέτη, υψώνουμε κάθε παράγοντα του γινομένου στον εκθέτη αυτό. (α · β)μ = αμ · βμ
(2 · 3)5 = 25 · 35, 25 · 35 = (2 · 3)5 = 65
- Για να υψώσουμε ένα πηλίκο σε έναν εκθέτη, υψώνουμε καθένα από τους όρους του πηλίκου στον εκθέτη αυτό. $$\left( \frac{ \alpha }{ \beta } \right)^{ \nu }$$ = $$ \frac{ \alpha ^{ \nu }}{ \beta ^{ \nu }} $$
$$ \frac{4}{25} = \frac{2^{2}}{5^{2}} =\left( \frac{2}{5} \right)^{2}$$
- Για να υψώσουμε μία δύναμη σε έναν εκθέτη, υψώνουμε τη βάση της δύναμης στο γινόμενο των εκθετών. $$\left( \alpha ^{ \mu }\right)^{ \nu }= \alpha ^{ \mu \cdot \nu }$$
$$4^{3}=\left(2^{2}\right)^{3}=2^{6}$$ |
|
