Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ
Τ |
|---|
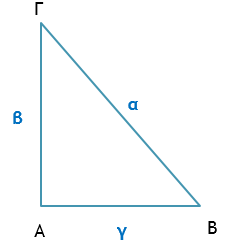
Τριγωνομετρικοί αριθμοίΟρισμοίΓια τις οξείες γωνίες ενός ορθογωνίου τριγώνου δίνονται οι εξής ορισμοί. $${\rm E}\Phi {\rm A}\Pi {\rm T}{\rm O}{\rm M}{\rm E}{\rm N}{\rm H} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}$$ $${\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$ $$\Sigma \Upsilon {\rm N}{\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$
$$\begin{array}{l}\varepsilon \varphi {\rm B} = \frac{{{\rm A}\Gamma }}{{{\rm A}{\rm B}}} = \frac{\beta }{\gamma }\,\,\,\,\,\,\,\,\,\,\,\,\varepsilon \varphi \Gamma = \frac{{{\rm A}{\rm B}}}{{{\rm A}\Gamma }} = \frac{\gamma }{\beta }\\\eta \mu {\rm B} = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\eta \mu \Gamma = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\\\sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\end{array}$$ Γνωρίζουμε ότι σε κάθε ορθογώνιο τρίγωνο η υποτείνουσα είναι μεγαλύτερη από καθεμία από τις κάθετες πλευρές. Επομένως ισχύουν οι ανισώσεις: 0 < ημω < 1 και 0 < συνω < 1
Σχέσεις τριγωνομετρικών αριθμώνΓια κάθε γωνία ισχύει ότι $$\varepsilon \varphi \omega = \frac{{\eta \mu \omega }}{{\sigma \upsilon \nu \omega }}\,\,\,\,\left\{ {\frac{{\eta \mu \Gamma }}{{\sigma \upsilon \nu \Gamma }} = \frac{{\frac{\gamma }{\alpha }}}{{\frac{\beta }{\alpha }}} = \frac{{\gamma \cdot \alpha }}{{\beta \cdot \alpha }} = \frac{\gamma }{\beta } = \varepsilon \varphi \Gamma } \right\}$$ Όπως φαίνεται $$\eta \mu {\rm B} = \sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,$$ και $$\eta \mu \Gamma = \sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }$$, δηλαδή το ημίτονο μιας γωνίας ισούται με το συνημίτονο της συμπληρωματικής της. Παρατηρήστε ότι $$\,\varepsilon \varphi \Gamma = \frac{1}{{\varepsilon \varphi {\rm B}}}$$, δηλαδή οι εφαπτομένες συμπληρωματικών γωνιών είναι αριθμοί αντίστροφοι, έχουν γινόμενο 1 $$\varepsilon \varphi {\rm B} \cdot \varepsilon \varphi \Gamma = \frac{\gamma }{\beta } \cdot \frac{\beta }{\gamma } = 1\,$$. Μεταβολές τριγωνομετρικών αριθμών οξειών γωνιώνΌταν μια οξεία γωνία αυξάνεται↑, τότε: αυξάνεται το ημίτονό↑ της, ελαττώνεται το συνημίτονό↓ της και αυξάνεται η εφαπτομένη↑ της. Χαρακτηριστικές τιμές τριγωνομετρικών αριθμών οξειών γωνιών$$\begin{array}{ccccccccccccccc}{}&{{{30}^o}}&{{{45}^o}}&{{{60}^o}}\\{\eta \mu }&{\frac{1}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 3 }}{2}}\\{\sigma \upsilon \nu }&{\frac{{\sqrt 3 }}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{1}{2}}\\{\varepsilon \varphi }&{\frac{{\sqrt 3 }}{3}}&1&{\sqrt 3 }\end{array}$$ | |