Το λεξικό "Μαθηματική ορολογία"


Το λεξικό "Μαθηματική ορολογία"

Περιήγηση στο γλωσσάριο χρησιμοποιώντας αυτό το ευρετήριο

Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ

Ε

Ε.Κ.Π.

Ε.Κ.Π. φυσικών αριθμών

Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) δύο ή περισσοτέρων φυσικών αριθμών που έχουν αναλυθεί σε γινόμενο πρώτων παραγόντων ονομάζεται, το γινόμενο των κοινών και μη κοινών παραγόντων τους με εκθέτη καθενός το μεγαλύτερο από τους εκθέτες του.

Παράδειγμα

Δίνονται οι αριθμοί 720, 540 και 360. Αναλύουμε τους αριθμούς σε γινόμενο πρώτων παραγόντων:

 

720 = 2·360 = 2·2·180 = 2·2·2·90 = 2·2·2·2·45 = 24·3·15 = 24·3·3·5 =  24·32·51

360 = 2·180 = 2·2·90 = 2·2·2·45 = 23·3·15 = 23·3·3·5 =  23·32·51

540 = 2·270 = 2·2·135 = 22·3·45 = 22·3·3·15 = 22·3·3·3·5 =  22·33·51

E.Κ.Π.(  720, 540, 630) = E.Κ.Π.( 24·32·51,  22·33·51, 23·32·51) = 24·33·51=2160

Ένας πιο απλός τρόπος:
  • Πολλαπλάσια 720 : 720 , 1440 , 2160 , 2880 ...
  • Πολλαπλάσια 360 : 360 , 720 , 1080 , 1440 , 1800 , 2160 , 2520 ...
  • Πολλαπλάσια 540 : 540 , 1080 , 1620 , 2160 , 2520 ..

 

 

Εμβαδόν

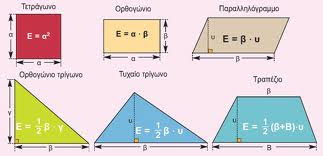
emvada.jpg

Εξίσωση

Ονομάζουμε εξίσωση την ισότητα δύο αλγεβρικών παραστάσεων που περιέχουν τουλάχιστον μια μεταβλητή που ονομάζεται άγνωστος.
π.χ. εξίσωση είναι η παράσταση 2x2+5x-3=8(x3+2)

  • Η αλγεβρική παράσταση αριστερά ή δεξιά του ίσον λέγεται μέλος της εξίσωσης.
  • Οι όροι που περιέχουν μεταβλητή λέγονται άγνωστοι όροι (2x2, 5x, x3), ενώ οι άλλοι λέγονται γνωστοί όροι.
  • Λύση ή ρίζα της εξίσωσης είναι η τιμή του αγνώστου που επαληθεύει την ισότητα.
  • Η διαδικασία αναζήτησης της λύσης της εξίσωσης θα λέγεται επίλυση της εξίσωσης.
Εξίσωση πρώτου βαθμού

Έχει τη μορφή beta x plus gamma space equals 0.

 

Αν Error converting from MathML to accessible text., τότε; η εξίσωση beta x plus gamma space equals 0 έχει μοναδική λύση την Error converting from MathML to accessible text..
Αν Error converting from MathML to accessible text., τότε η εξίσωση beta x plus gamma space equals 0 γράφεται Error converting from MathML to accessible text. και

  • αν Error converting from MathML to accessible text. δεν έχει λύση (αδύνατη) 0x=γ, ενώ 
  • αν Error converting from MathML to accessible text., κάθε αριθμός είναι λύση της (ταυτότητα ή αόριστη). 0x=0 

 Δες σε παράδειγμα τον αλγόριθμο επίλυσης εξίσωσης πρώτου βαθμού ... εδώ.

Δες σε παράδειγμα τη διαδικασία επίλυσης προβλήματος με τη χρήση εξίσωσης πρώτου βαθμού ... εδώ.

 

Ευθεία

Οι γραφικές παραστάσεις των ακόλουθων συναρτήσεων είναι ευθείες γραμμές:

Η γραφική παράσταση είναι ευθεία γραμμήbold italic x bold equals bold italic lambda  Ευθεία παράλληλη στον άξονα bold italic y που περνά από το σημείο bold left parenthesis bold italic lambda bold comma bold 0 bold right parenthesis

bold italic y bold equals bold italic beta  Ευθεία παράλληλη στον άξονα bold italic x που περνά από το σημείο bold left parenthesis bold 0 bold comma bold italic beta bold right parenthesis

bold italic y bold equals bold italic alpha bold italic x  Ευθεία με κλίση bold italic alpha  που περνά από το σημείο bold left parenthesis bold 0 bold comma bold 0 bold right parenthesis, την αρχή των αξόνων. Είναι η γραφική παράσταση των ανάλογων μεγεθών.

bold italic y bold equals bold italic alpha bold italic x bold plus bold italic beta  Ευθεία με κλίση bold italic alpha  που τον άξονα bold italic x στο σημείο bold italic capital lambda open parentheses bold minus bold beta over bold alpha bold comma bold 0 close parentheses και τον άξονα bold italic y στο σημείο bold italic capital kappa open parentheses bold 0 bold comma bold italic beta close parentheses

 

Δείτε περισσότερα... εδώ.