Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ
Δ |
|---|
ΔιάνυσμαΟρισμοί
Διανύσματα που έχουν την ίδια διεύθυνση. Ομόρροπα - Αντίρροπα, Ίσα - Αντίθετα
Δύο διανύσματα λέγονται ίσα, όταν έχουν την ίδια διεύθυνση, την ίδια φορά και ίσα μέτρα.
Αντίρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και αντίθετη φορά (αντίθετη κατεύθυνση) Δύο διανύσματα είναι αντίθετα, όταν έχουν την ίδια διεύθυνση, ίσα μέτρα και αντίθετη φορά. ΠΡΟΣΟΧΗ: (Τα διανύσματα $$\overrightarrow {{\rm A}{\rm B}} $$ και $$\overrightarrow {{\rm B}{\rm A}} $$ είναι αντίθετα $$\overrightarrow {{\rm A}{\rm B}} = - \overrightarrow {{\rm B}{\rm A}} $$. Έχουν την ίδια διεύθυνση, αντίθετες φορές και ίσα μέτρα $$\left| {\overrightarrow {{\rm A}{\rm B}} } \right| = \left| {\overrightarrow {{\rm B}{\rm A}} } \right|$$). Πρόσθεση διανυσμάτωνΚανόνας παραλληλογράμμου
Κανόνας πολυγώνου
Στο σχήμα ισχύει ότι $$\overrightarrow \alpha + \overrightarrow \beta + \overrightarrow \gamma = \overrightarrow \delta $$.
Αφαίρεση διανυσμάτων
Μηδενικό διάνυσμαΤο μηδενικό διάνυσμα είναι ένα διάνυσμα του οποίου η αρχή και το τέλος (πέρας) ταυτίζονται. Το μηδενικό διάνυσμα συμβολίζεται με $$\overrightarrow 0 $$. Κάθετα διανύσματα. Σύνθεση - Ανάλυση Ουσιαστικά αντικαθιστούμε τα δυο διανύσματα $$\overrightarrow \alpha $$, $$\overrightarrow \beta $$ με ένα $$\overrightarrow \gamma $$ ώστε $$\overrightarrow \alpha + \overrightarrow \beta = \overrightarrow \gamma $$.
Ανάλυση διανύσματος σε δυο συνιστώσες. Αντικαθιστούμε ένα διάνυσμα $$\overrightarrow \gamma $$ με δυο κάθετες συνιστώσες $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$, που έχουν το αρχικό διάνυσμα ως άθροισμα. Χρησιμοποιούνται οι Τριγωνομετρικοί αριθμοί και προκύπτει ότι:
| |
ΔύναμηΔυνάμεις ρητών αριθμών με φυσικό εκθέτη
Πρόσημο δύναμης
Δυνάμεις ρητών αριθμών με ακέραιο εκθέτη
$$\left( \frac{ \alpha }{ \beta } \right)^{-\ ν}$$=$$\left( \frac{ \beta }{ \alpha } \right)^{\ ν}$$ , $$\left( \frac{ 2 }{ 3 } \right)^{-\ 5}$$=$$\left( \frac{ 3 }{ 2 } \right)^{\ 5}$$
Ιδιότητες δυνάμεων
32 · 33 = 35, 32 · 3- 3 = 3- 1 = $$ \frac{1}{3} $$
32 : 33 = 3-1 = $$ \frac{1}{3} $$, 32 : 3- 3 = 32 - (-3) = 35
(2 · 3)5 = 25 · 35, 25 · 35 = (2 · 3)5 = 65
$$ \frac{4}{25} = \frac{2^{2}}{5^{2}} =\left( \frac{2}{5} \right)^{2}$$
$$4^{3}=\left(2^{2}\right)^{3}=2^{6}$$ | |
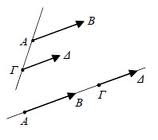 Ομόρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και την ίδια φορά (ἰδια κατεύθυνση)
Ομόρροπα λέγονται τα διανύσματα που έχουν την ίδια διεύθυνση και την ίδια φορά (ἰδια κατεύθυνση)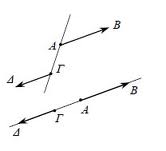
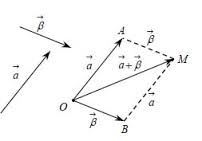 Μεταφέρουμε τα διανύσματα, έτσι ώστε να έχουν κοινή αρχή και σχηματίζουμε το παραλληλόγραμμο που έχει πλευρές τα διανύσματα. Η διαγώνιος του παραλληλογράμμου που έχει ως αρχή την κοινή τους αρχή είναι το άθροισμα των διανυσμάτων.
Μεταφέρουμε τα διανύσματα, έτσι ώστε να έχουν κοινή αρχή και σχηματίζουμε το παραλληλόγραμμο που έχει πλευρές τα διανύσματα. Η διαγώνιος του παραλληλογράμμου που έχει ως αρχή την κοινή τους αρχή είναι το άθροισμα των διανυσμάτων. 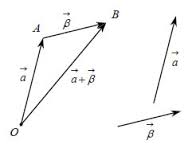
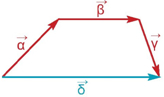 Μεταφέρουμε παράλληλα τα διανύσματα που θέλουμε να προσθέσουμε, ώστε να γίνουν όλα διαδοχικά. Το άθροισμα των θα είναι το
Μεταφέρουμε παράλληλα τα διανύσματα που θέλουμε να προσθέσουμε, ώστε να γίνουν όλα διαδοχικά. Το άθροισμα των θα είναι το 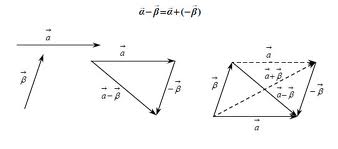 Η διαφορά δύο διανυσμάτων $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$ συμβολίζεται με $$\overrightarrow \alpha - \overrightarrow \beta $$ και ορίζεται ως άθροισμα του $$\overrightarrow \alpha $$ με το αντίθετο
Η διαφορά δύο διανυσμάτων $$\overrightarrow \alpha $$ και $$\overrightarrow \beta $$ συμβολίζεται με $$\overrightarrow \alpha - \overrightarrow \beta $$ και ορίζεται ως άθροισμα του $$\overrightarrow \alpha $$ με το αντίθετο 