Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ
Μ |
|---|
Μεταβλητήλέγεται ένα γράμμα π.χ x,y,z,ω,…( ελληνικό ή λατινικό) που παριστάνει έναν οποιοδήποτε αριθμό. Χρησιμοποιώντας μεταβλητές "μεταφράζουμε" μια φράση σε Αλγεβρική παράσταση. Παράδειγμα: Το άθροισμα δύο αριθμών πολλαπλασιασμένο επί 9. Αν συμβολίσουμε τους αριθμούς x και y τότε το άθροισμά τους είναι x+y και η ζητούμενη αλγεβρική παράσταση 9(x+y).
| |
Π |
|---|
Πραγματικοί αριθμοίΟι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς Άξονας πραγματικών αριθμών
Οι ακέραιοι αριθμοί: ... -3, -2, -1, 0, 1, 2, 3 ... παριστάνονται πάλι με σημεία. Το σύνολο των ρητών αριθμών, δηλαδή των αριθμών που μπορούν να γραφούν στη μορφή, όπου μ ακέραιος και ν φυσικός αριθμός. Οι ρητοί αριθμοί έχουν γνωστή δεκαδική μορφή και γεμίζουν την ευθεία, αλλά όχι πλήρως. Οι πραγματικοί αριθμοί αποτελούνται όχι μόνο από τους ρητούς αλλά και όλους τους άρρητους.
| |
ΠρίσμαΚάθε πρίσμα έχει: δύο έδρες παράλληλες, που είναι ίσα πολύγωνα και τις άλλες έδρες του που είναι ορθογώνια παραλληλόγραμμα και ονομάζονται παράπλευρες έδρες. Οι δύο παράλληλες έδρες του λέγονται βάσεις του πρίσματος. Οι παράπλευρες έδρες σχηματίζουν την παράπλευρη επιφάνεια του πρίσματος. Οι πλευρές των εδρών του πρίσματος ονομάζονται ακμές.
Περισσότερα... | |
Πυθαγόρειο θεώρημα
ΒΓ2 = ΑΒ2 + ΑΓ2α2 = β2 + γ2
Αντίστροφο Πυθαγόρειο θεώρημα Αν ισχύει η σχέση ΚΛ2 = ΜΛ2 + ΜΚ2 μεταξύ των πλευρών ενός τριγώνου ΚΛΜ , τότε το τρίγωνο είναι ορθογώνιο με ορθή γωνία τη γωνία Μ. | |
ΠυραμίδαΗ πυραμίδα είναι γεωμετρικό στερεό. Είναι πολύεδρο που σχηματίζεται με ένα ν-γωνο ως βάση και ν τριγωνικές πλευρές που συνδέονται σε μια κορυφή. Περισσότερα... | |
Ρ |
|---|
Ρητοί αριθμοί
Μορφή ρητού αριθμού: $$ \frac{ \mu }{ \nu } $$ με ν ≠ 0 κια Μ.Κ.Δ. (μ,ν) =1 Κάθε ρητός αριθμός μπορεί να γραφεί και σε δεκαδική μορφή. Αυτό γίνεται κάνοντας τη διαίρεση μ / ν. Η διαίρεση αυτή μπορεί
Οι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς
| |
Σ |
|---|
ΣφαίραΣφαίρα λέγεται το στερεό σώμα που παράγεται, αν περιστρέψουμε ένα κυκλικό δίσκο (Ο, ρ) γύρω από μία διάμετρό του.
Περισσότερα... | |
Τ |
|---|
Τετραγωνική ρίζαΤετρ. ρίζα ενός θετικού αριθμού α, λέγεται ο θετικός αριθμός, ο οποίος, όταν υψωθεί στο τετράγωνο, δίνει τον αριθμό α. Η τετρ. ρίζα του α συμβολίζεται με $$ \sqrt{ \alpha } $$.
Ιδιότητες
Προσοχή!
Χρήσιμες ιδιότητες για την απλοποίηση παραστάσεων Ρίζα δύναμης με άρτιο εκθέτη: $$\sqrt {{\alpha ^{2\nu }}} = \sqrt {{{\left( {{\alpha ^\nu }} \right)}^2}} = {\alpha ^\nu }$$
| |
Τριγωνομετρικοί αριθμοίΟρισμοίΓια τις οξείες γωνίες ενός ορθογωνίου τριγώνου δίνονται οι εξής ορισμοί. $${\rm E}\Phi {\rm A}\Pi {\rm T}{\rm O}{\rm M}{\rm E}{\rm N}{\rm H} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}$$ $${\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$ $$\Sigma \Upsilon {\rm N}{\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$
$$\begin{array}{l}\varepsilon \varphi {\rm B} = \frac{{{\rm A}\Gamma }}{{{\rm A}{\rm B}}} = \frac{\beta }{\gamma }\,\,\,\,\,\,\,\,\,\,\,\,\varepsilon \varphi \Gamma = \frac{{{\rm A}{\rm B}}}{{{\rm A}\Gamma }} = \frac{\gamma }{\beta }\\\eta \mu {\rm B} = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\eta \mu \Gamma = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\\\sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\end{array}$$ Γνωρίζουμε ότι σε κάθε ορθογώνιο τρίγωνο η υποτείνουσα είναι μεγαλύτερη από καθεμία από τις κάθετες πλευρές. Επομένως ισχύουν οι ανισώσεις: 0 < ημω < 1 και 0 < συνω < 1
Σχέσεις τριγωνομετρικών αριθμώνΓια κάθε γωνία ισχύει ότι $$\varepsilon \varphi \omega = \frac{{\eta \mu \omega }}{{\sigma \upsilon \nu \omega }}\,\,\,\,\left\{ {\frac{{\eta \mu \Gamma }}{{\sigma \upsilon \nu \Gamma }} = \frac{{\frac{\gamma }{\alpha }}}{{\frac{\beta }{\alpha }}} = \frac{{\gamma \cdot \alpha }}{{\beta \cdot \alpha }} = \frac{\gamma }{\beta } = \varepsilon \varphi \Gamma } \right\}$$ Όπως φαίνεται $$\eta \mu {\rm B} = \sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,$$ και $$\eta \mu \Gamma = \sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }$$, δηλαδή το ημίτονο μιας γωνίας ισούται με το συνημίτονο της συμπληρωματικής της. Παρατηρήστε ότι $$\,\varepsilon \varphi \Gamma = \frac{1}{{\varepsilon \varphi {\rm B}}}$$, δηλαδή οι εφαπτομένες συμπληρωματικών γωνιών είναι αριθμοί αντίστροφοι, έχουν γινόμενο 1 $$\varepsilon \varphi {\rm B} \cdot \varepsilon \varphi \Gamma = \frac{\gamma }{\beta } \cdot \frac{\beta }{\gamma } = 1\,$$. Μεταβολές τριγωνομετρικών αριθμών οξειών γωνιώνΌταν μια οξεία γωνία αυξάνεται↑, τότε: αυξάνεται το ημίτονό↑ της, ελαττώνεται το συνημίτονό↓ της και αυξάνεται η εφαπτομένη↑ της. Χαρακτηριστικές τιμές τριγωνομετρικών αριθμών οξειών γωνιών$$\begin{array}{ccccccccccccccc}{}&{{{30}^o}}&{{{45}^o}}&{{{60}^o}}\\{\eta \mu }&{\frac{1}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 3 }}{2}}\\{\sigma \upsilon \nu }&{\frac{{\sqrt 3 }}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{1}{2}}\\{\varepsilon \varphi }&{\frac{{\sqrt 3 }}{3}}&1&{\sqrt 3 }\end{array}$$ | |
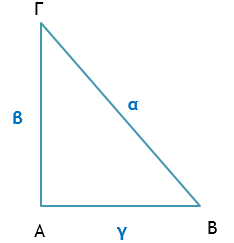 Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.
Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.