Το λεξικό "Μαθηματική ορολογία"
Το λεξικό "Μαθηματική ορολογία"
Ειδικά | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π | Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ΟΛΑ
Α |
|---|
Ακέραιοι αριθμοί
Οι Φυσικοί αριθμοί περιέχονται στους ακεραίους αριθμούς | |
Αναγωγή ομοίων όρωνΗ διαδικασία αυτή με την οποία γράφουμε σε απλούστερη μορφή αλγεβρικές παραστάσεις, ονομάζεται «αναγωγή ομοίων όρων». Βασίζεται στην Eπιμεριστική ιδιότητα. 7 · α + 8 · α = (7 + 8) · α = 15 · α | |
ΑνισότηταΣύγκρισηΓια να συγκρίνουμε λοιπόν δύο πραγματικούς αριθμούς α και β, που δεν έχουν παρασταθεί με σημεία ενός άξονα, βρίσκουμε τη διαφορά τους α - β και εξετάζουμε αν είναι θετική ή αρνητική ή μηδέν. Αν α - β > 0 τότε α > β Διάταξη
Δύο ή περισσότεροι πραγματικοί αριθμοί που έχουν παρασταθεί με σημεία ενός άξονα είναι διατεταγμένοι. Άρα: Κάθε θετικός αριθμός είναι μεγαλύτερος από το μηδέν. Ιδιότητες ανισότητας- διάταξης
Αν α > β και γ > 0 τότε α γ > β γ και $$ \frac{ \alpha }{ \gamma } > \frac{ \beta }{ \gamma } $$. Αν πολλαπλασιάσουμε ή διαιρέσουμε και τα δύο μέλη μιας ανισότητας με τον ίδιο θετικό αριθμό, τότε προκύπτει ανισότητα με την ίδια φορά. Αν α > β και γ < 0 τότε α γ < β γ και $$ \frac{ \alpha }{ \gamma } < \frac{ \beta }{ \gamma } $$. Αν πολλαπλασιάσουμε ή διαιρέσουμε και τα δύο μέλη μιας ανισότητας με τον ίδιο αρνητικό αριθμό, τότε προκύπτει ανισότητα αντίθετης φοράς Αν α > β και γ > δ τότε α + γ > β + δ. Αν προσθέσουμε κατά μέλη δύο ή περισσότερες ανισότητες που έχουν την ίδια φορά, τότε προκύπτει ανισότητα με την ίδια φορά.. Αν α, β, γ, δ θετικοί αριθμοί με α > β και γ > δ τότε αγ > βδ. Αν πολλαπλασιάσουμε κατά μέλη δύο ή περισσότερες ανισότητες που έχουν την ίδια φορά και θετικά μέλη, τότε προκύπτει ανισότητα με την ίδια φορά. α2 ≥ 0. Το τετράγωνο κάθε πραγματικού αριθμού α είναι μη αρνητικός αριθμός. Αν για τους πραγματικούς αριθμούς α, β ισχύει α2 + β2 = 0, τότε α = 0 και β = 0. Αν α > β και β > γ τότε α > γ. Μεταβατική ιδιότητα. Δείτε παράδειγμα ασκήσεων με ανισώσεις ... εδώ.
| |
ΑνίσωσηΟνομάζουμε ανίσωση την ανισότητα δύο αλγεβρικών παραστάσεων που περιέχουν τουλάχιστον μια μεταβλητή που ονομάζεται άγνωστος. π.χ. ανίσωση είναι η παράσταση 2x+5x-3≥8(x+2)
Δείτε παράδειγμα ασκήσεων με ανισώσεις ... εδώ. | |
Απόλυτη τιμή
Αντίθετοι ονομάζονται δύο αριθμοί που είναι ετερόσημοι και έχουν την ίδια απόλυτη τιμή. Ο αντίθετος του x είναι ο -x. H απόλυτη τιμή ενός θετικού αριθμού είναι ο ίδιος ο αριθμός. |+6| = 6. H απόλυτη τιμή ενός αρνητικού αριθμού είναι ο αντίθετός του. |-6| = -(6-)=6 H απόλυτη τιμή του μηδενός είναι το μηδέν. | |
Αριθμητική παράστασηονομάζεται μια παράσταση που περιέχει πράξεις με αριθμούς.. | |
Αρνητικοί αριθμοίΟι αρνητικοί αριθμοί με πρόσημο - , είναι οι συμμετρικοί των θετικών αριθμών, με πρόσημο + (το οποίο παραλείπεται όταν δε δημιουργείται ασάφεια.
Παράσταση των ρητών αριθμών με σημεία μιας ευθείαςΑν θεωρήσουμε αριστερά της αρχής Ο του ημιάξονα Οx των αριθμών, τον αντικείμενο αυτού ημιάξονα Οx', θα έχουμε τη δυνατότητα, με αυτόν τον τρόπο, να παραστήσουμε όλους τους ρητούς αριθμούς. Το σημείο Α έχει τετμημένη 4 και το σημείο Β έχει τετμημένη -2. Απόλυτη τιμή Πράξεις με αρνητικούς αριθμούςΠρόσθεση
Αφαίρεση
Πολλαπλασιασμός
Διαίρεση
| |
Ά |
|---|
Άρρητοι αριθμοί
| |
Δ |
|---|
Διάμεσος παρατηρήσεων
Η διάμεσος «προσεγγίζει» καλύτερα την τιμή που έχουν οι περισσότερες παρατηρήσεις. | |
Διάμεσος τριγώνου
| |
ΔύναμηΔυνάμεις ρητών αριθμών με φυσικό εκθέτη
Πρόσημο δύναμης
Δυνάμεις ρητών αριθμών με ακέραιο εκθέτη
$$\left( \frac{ \alpha }{ \beta } \right)^{-\ ν}$$=$$\left( \frac{ \beta }{ \alpha } \right)^{\ ν}$$ , $$\left( \frac{ 2 }{ 3 } \right)^{-\ 5}$$=$$\left( \frac{ 3 }{ 2 } \right)^{\ 5}$$
Ιδιότητες δυνάμεων
32 · 33 = 35, 32 · 3- 3 = 3- 1 = $$ \frac{1}{3} $$
32 : 33 = 3-1 = $$ \frac{1}{3} $$, 32 : 3- 3 = 32 - (-3) = 35
(2 · 3)5 = 25 · 35, 25 · 35 = (2 · 3)5 = 65
$$ \frac{4}{25} = \frac{2^{2}}{5^{2}} =\left( \frac{2}{5} \right)^{2}$$
$$4^{3}=\left(2^{2}\right)^{3}=2^{6}$$ | |
Ε |
|---|
Ε.Κ.Π.Ε.Κ.Π. φυσικών αριθμώνΕλάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) δύο ή περισσοτέρων φυσικών αριθμών που έχουν αναλυθεί σε γινόμενο πρώτων παραγόντων ονομάζεται, το γινόμενο των κοινών και μη κοινών παραγόντων τους με εκθέτη καθενός το μεγαλύτερο από τους εκθέτες του. Παράδειγμα Δίνονται οι αριθμοί 720, 540 και 360. Αναλύουμε τους αριθμούς σε γινόμενο πρώτων παραγόντων:
720 = 2·360 = 2·2·180 = 2·2·2·90 = 2·2·2·2·45 = 24·3·15 = 24·3·3·5 = 24·32·51 360 = 2·180 = 2·2·90 = 2·2·2·45 = 23·3·15 = 23·3·3·5 = 23·32·51 540 = 2·270 = 2·2·135 = 22·3·45 = 22·3·3·15 = 22·3·3·3·5 = 22·33·51 E.Κ.Π.( 720, 540, 630) = E.Κ.Π.( 24·32·51, 22·33·51, 23·32·51) = 24·33·51=2160 Ένας πιο απλός τρόπος:
| |
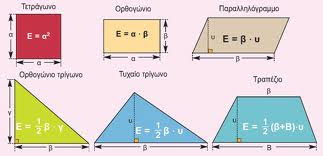
Εμβαδόν
| |
ΕξίσωσηΟνομάζουμε εξίσωση την ισότητα δύο αλγεβρικών παραστάσεων που περιέχουν τουλάχιστον μια μεταβλητή που ονομάζεται άγνωστος.
Εξίσωση πρώτου βαθμούΈχει τη μορφή
Αν
Δες σε παράδειγμα τον αλγόριθμο επίλυσης εξίσωσης πρώτου βαθμού ... εδώ. Δες σε παράδειγμα τη διαδικασία επίλυσης προβλήματος με τη χρήση εξίσωσης πρώτου βαθμού ... εδώ. | |
ΕυθείαΟι γραφικές παραστάσεις των ακόλουθων συναρτήσεων είναι ευθείες γραμμές:
Δείτε περισσότερα... εδώ. | |
Ι |
|---|
ΙδιότηταΙδιότητες των πράξεωνΟυδέτερο στοιχείο
Καταστροφικό στοιχείο
Απαγορεύεται
Αντίθετοι αριθμοί
Αντίστροφοι αριθμοί
Αντιμεταθετική ιδιότητα
Προσεταιριστική ιδιότητα
Επιμεριστική ιδιότητα του πολλαπλασιασμού ως προς
| |
ΙσότηταΙδιότητες ισότηταςΧρήσιμες ιδιότητες πράξεων | |
Κ |
|---|
ΚύλινδροςΈνας κύλινδρος αποτελείται από δύο ίσους και παράλληλους κυκλικούς δίσκους, που είναι οι βάσεις του, και την παράπλευρη επιφάνεια, που, αν την ξετυλίξουμε, θα δούμε ότι έχει σχήμα ορθογωνίου. Η απόσταση των δύο βάσεων λέγεται ύψος του κυλίνδρου.
Περισσότερα... | |
Μ |
|---|
Μ.Κ.Δ.Μ.Κ.Δ. φυσικών αριθμώνΜέγιστος Κοινός Διαιρέτης ( Μ.Κ.Δ. ) δύο ή περισσοτέρων φυσικών αριθμών που έχουν αναλυθεί σε γινόμενο πρώτων παραγόντων ονομάζεται, το γινόμενο των κοινών παραγόντων τους με εκθέτη καθενός το μικρότερο από τους εκθέτες του. Παράδειγμα Για μα βρούμε τον Μέγιστο Κοινό Διαιρέτη των αριθμών αναλύουμε τους αριθμούς σε γινόμενο πρώτων παραγόντων:
720 = 2·360 = 2·2·180 = 2·2·2·90 = 2·2·2·2·45 = 24·3·15 = 24·3·3·5 = 24·32·51 360 = 2·180 = 2·2·90 = 2·2·2·45 = 23·3·15 = 23·3·3·5 = 23·32·51 540 = 2·270 = 2·2·135 = 22·3·45 = 22·3·3·15 = 22·3·3·3·5 = 22·33·51
Μ.Κ.Δ.( 720, 540, 630) = Μ.Κ.Δ.( 24·32·51, 22·33·51, 23·32·51) = 22·32·51 = 180 Ένας πιο απλός τρόπος:
| ||||||||||||
Μέση τιμήΜέσος όρος, Μέση τιμήΓια να βρούμε τη μέση τιμή ενός συνόλου παρατηρήσεων, προσθέτουμε όλες τις παρατηρήσεις και διαιρούμε με το πλήθος των παρατηρήσεων αυτών. Η μέση τιμή δεν μπορεί να είναι μικρότερη από τη μικρότερη των τιμών ή μεγαλύτερη από τη μεγαλύτερη, επηρεάζεται δε σημαντικά από τις μεγάλες τιμές. | |
Μεταβλητήλέγεται ένα γράμμα π.χ x,y,z,ω,…( ελληνικό ή λατινικό) που παριστάνει έναν οποιοδήποτε αριθμό. Χρησιμοποιώντας μεταβλητές "μεταφράζουμε" μια φράση σε Αλγεβρική παράσταση. Παράδειγμα: Το άθροισμα δύο αριθμών πολλαπλασιασμένο επί 9. Αν συμβολίσουμε τους αριθμούς x και y τότε το άθροισμά τους είναι x+y και η ζητούμενη αλγεβρική παράσταση 9(x+y).
| |
Π |
|---|
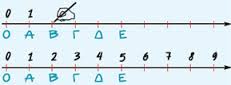
Πραγματικοί αριθμοίΟι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς Άξονας πραγματικών αριθμών
Οι ακέραιοι αριθμοί: ... -3, -2, -1, 0, 1, 2, 3 ... παριστάνονται πάλι με σημεία. Το σύνολο των ρητών αριθμών, δηλαδή των αριθμών που μπορούν να γραφούν στη μορφή, όπου μ ακέραιος και ν φυσικός αριθμός. Οι ρητοί αριθμοί έχουν γνωστή δεκαδική μορφή και γεμίζουν την ευθεία, αλλά όχι πλήρως. Οι πραγματικοί αριθμοί αποτελούνται όχι μόνο από τους ρητούς αλλά και όλους τους άρρητους.
| |
ΠρίσμαΚάθε πρίσμα έχει: δύο έδρες παράλληλες, που είναι ίσα πολύγωνα και τις άλλες έδρες του που είναι ορθογώνια παραλληλόγραμμα και ονομάζονται παράπλευρες έδρες. Οι δύο παράλληλες έδρες του λέγονται βάσεις του πρίσματος. Οι παράπλευρες έδρες σχηματίζουν την παράπλευρη επιφάνεια του πρίσματος. Οι πλευρές των εδρών του πρίσματος ονομάζονται ακμές.
Περισσότερα... | |
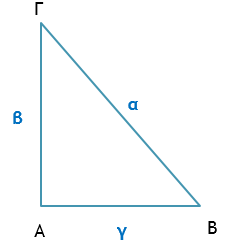
Πυθαγόρειο θεώρημα
ΒΓ2 = ΑΒ2 + ΑΓ2α2 = β2 + γ2
Αντίστροφο Πυθαγόρειο θεώρημα Αν ισχύει η σχέση ΚΛ2 = ΜΛ2 + ΜΚ2 μεταξύ των πλευρών ενός τριγώνου ΚΛΜ , τότε το τρίγωνο είναι ορθογώνιο με ορθή γωνία τη γωνία Μ. | |
ΠυραμίδαΗ πυραμίδα είναι γεωμετρικό στερεό. Είναι πολύεδρο που σχηματίζεται με ένα ν-γωνο ως βάση και ν τριγωνικές πλευρές που συνδέονται σε μια κορυφή. Περισσότερα... | |
Ρ |
|---|
Ρητοί αριθμοί
Μορφή ρητού αριθμού: $$ \frac{ \mu }{ \nu } $$ με ν ≠ 0 κια Μ.Κ.Δ. (μ,ν) =1 Κάθε ρητός αριθμός μπορεί να γραφεί και σε δεκαδική μορφή. Αυτό γίνεται κάνοντας τη διαίρεση μ / ν. Η διαίρεση αυτή μπορεί
Οι Φυσικοί αριθμοί περιέχονται στους ρητούς αριθμούς
| |
Σ |
|---|
ΣφαίραΣφαίρα λέγεται το στερεό σώμα που παράγεται, αν περιστρέψουμε ένα κυκλικό δίσκο (Ο, ρ) γύρω από μία διάμετρό του.
Περισσότερα... | |
Τ |
|---|
Τετραγωνική ρίζαΤετρ. ρίζα ενός θετικού αριθμού α, λέγεται ο θετικός αριθμός, ο οποίος, όταν υψωθεί στο τετράγωνο, δίνει τον αριθμό α. Η τετρ. ρίζα του α συμβολίζεται με $$ \sqrt{ \alpha } $$.
Ιδιότητες
Προσοχή!
Χρήσιμες ιδιότητες για την απλοποίηση παραστάσεων Ρίζα δύναμης με άρτιο εκθέτη: $$\sqrt {{\alpha ^{2\nu }}} = \sqrt {{{\left( {{\alpha ^\nu }} \right)}^2}} = {\alpha ^\nu }$$
| |
Τριγωνομετρικοί αριθμοίΟρισμοίΓια τις οξείες γωνίες ενός ορθογωνίου τριγώνου δίνονται οι εξής ορισμοί. $${\rm E}\Phi {\rm A}\Pi {\rm T}{\rm O}{\rm M}{\rm E}{\rm N}{\rm H} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}$$ $${\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{{\rm A}\Pi {\rm E}{\rm N}{\rm A}{\rm N}{\rm T}{\rm I}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$ $$\Sigma \Upsilon {\rm N}{\rm H}{\rm M}{\rm I}{\rm T}{\rm O}{\rm N}{\rm O} = \frac{{\Pi {\rm P}{\rm O}\Sigma {\rm K}{\rm E}{\rm I}{\rm M}{\rm E}{\rm N}{\rm H}\,\,{\rm K}{\rm A}\Theta {\rm E}{\rm T}{\rm H}}}{{\Upsilon \Pi {\rm O}{\rm T}{\rm E}{\rm I}{\rm N}{\rm O}\Upsilon \Sigma {\rm A}}}$$
$$\begin{array}{l}\varepsilon \varphi {\rm B} = \frac{{{\rm A}\Gamma }}{{{\rm A}{\rm B}}} = \frac{\beta }{\gamma }\,\,\,\,\,\,\,\,\,\,\,\,\varepsilon \varphi \Gamma = \frac{{{\rm A}{\rm B}}}{{{\rm A}\Gamma }} = \frac{\gamma }{\beta }\\\eta \mu {\rm B} = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\eta \mu \Gamma = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\\\sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }\,\,\,\,\,\,\,\,\,\,\,\,\sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\end{array}$$ Γνωρίζουμε ότι σε κάθε ορθογώνιο τρίγωνο η υποτείνουσα είναι μεγαλύτερη από καθεμία από τις κάθετες πλευρές. Επομένως ισχύουν οι ανισώσεις: 0 < ημω < 1 και 0 < συνω < 1
Σχέσεις τριγωνομετρικών αριθμώνΓια κάθε γωνία ισχύει ότι $$\varepsilon \varphi \omega = \frac{{\eta \mu \omega }}{{\sigma \upsilon \nu \omega }}\,\,\,\,\left\{ {\frac{{\eta \mu \Gamma }}{{\sigma \upsilon \nu \Gamma }} = \frac{{\frac{\gamma }{\alpha }}}{{\frac{\beta }{\alpha }}} = \frac{{\gamma \cdot \alpha }}{{\beta \cdot \alpha }} = \frac{\gamma }{\beta } = \varepsilon \varphi \Gamma } \right\}$$ Όπως φαίνεται $$\eta \mu {\rm B} = \sigma \upsilon \nu \Gamma = \frac{{{\rm A}\Gamma }}{{\Gamma {\rm B}}} = \frac{\beta }{\alpha }\,$$ και $$\eta \mu \Gamma = \sigma \upsilon \nu {\rm B} = \frac{{{\rm A}{\rm B}}}{{\Gamma {\rm B}}} = \frac{\gamma }{\alpha }$$, δηλαδή το ημίτονο μιας γωνίας ισούται με το συνημίτονο της συμπληρωματικής της. Παρατηρήστε ότι $$\,\varepsilon \varphi \Gamma = \frac{1}{{\varepsilon \varphi {\rm B}}}$$, δηλαδή οι εφαπτομένες συμπληρωματικών γωνιών είναι αριθμοί αντίστροφοι, έχουν γινόμενο 1 $$\varepsilon \varphi {\rm B} \cdot \varepsilon \varphi \Gamma = \frac{\gamma }{\beta } \cdot \frac{\beta }{\gamma } = 1\,$$. Μεταβολές τριγωνομετρικών αριθμών οξειών γωνιώνΌταν μια οξεία γωνία αυξάνεται↑, τότε: αυξάνεται το ημίτονό↑ της, ελαττώνεται το συνημίτονό↓ της και αυξάνεται η εφαπτομένη↑ της. Χαρακτηριστικές τιμές τριγωνομετρικών αριθμών οξειών γωνιών$$\begin{array}{ccccccccccccccc}{}&{{{30}^o}}&{{{45}^o}}&{{{60}^o}}\\{\eta \mu }&{\frac{1}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 3 }}{2}}\\{\sigma \upsilon \nu }&{\frac{{\sqrt 3 }}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{1}{2}}\\{\varepsilon \varphi }&{\frac{{\sqrt 3 }}{3}}&1&{\sqrt 3 }\end{array}$$ | |
Υ |
|---|
Υπερβολή
Και στις δύο περιπτώσεις η γραφική παράσταση μιας υπερβολής έχει:
Όταν οι μεταβλητές x , y εκφράζουν ποσά / μεγέθη, τότε τα ποσά / μεγέθη αυτά είναι αντιστρόφως ανάλογα, το γινόμενό τους είναι η σταθερά α. Δεἰτε ένα παράδειγμα αντιστρόφως ποσών και τη μελέτη με τη χρήση συναρτήσεων και γραφικών... εδώ. | |
Φ |
|---|
Φυσικοί αριθμοίΟι αριθμοί 0, 1, 2, 3, 4, 5, 6......... 98, 99, 100........ 1999, 2000, 2001, ... ονομάζονται φυσικοί αριθμοί.
Κάθε φυσικός αριθμός έχει έναν επόμενο και ένα προηγούμενο φυσικό αριθμό, εκτός από το 0 που έχει μόνο επόμενο, το 1. Περισσότερα... | |


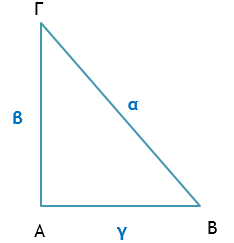 Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.
Το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών του.